Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
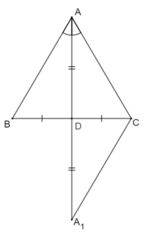
- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)
⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ 
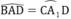(hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
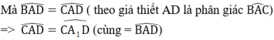
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
Nếu tam giác ABC có AM vừa là đường cao,vừa là đường trung tuyến và thì tam giác ABC là một tam giác cân tại đỉnh A
Nếu thấy bài làm của mình đúng thì tick nha bạn.
Nhân dịp năm mới mình chúc bạn 1 năm mạnh khoẻ,vui vẻ ,học giỏi nha.
Nếu tam giác ABC có AM vừa là đường cao, vừa là đường trung tuyến và góc BAC = 50 độ thì góc ABC = ?
Tam giác ABC có AM vừa là đường cao, vừa là đường trung tuyến
=> tam giác ABC cân tại A.
vậy góc ABC= (180-50):2=65
Tam giác ABC có AM vừa là đường cao, vừa là đường trung tuyến => tam giác ABC cân tại A.
vậy góc ABC= (180-50):2=65
Tam giác ABC có AM vừa là đường cao,vừa là đường trung tuyến
=> tam giác ABC cân tại A
=> AB = AC
góc ABC = góc ACB *
Ta có : góc BAC + góc ABC + góc ACB = 180 độ ( ĐL tổng 3 góc trong tam giác )
Mà : góc BAC = 50 độ
=> góc ABC + góc ACB = 180 - 50
=> góc ABC + góc ACB = 130 độ
Mà : ( theo * )
=> góc ABC = góc ACB = \(\frac{130}{2}\) = 65 độ
=> góc ABC = 65 độ
cứu
sửa đề tam giác DEF là tam giác gì ?
Vì tam giác DEF có DM là đường trung tuyến
đồng thời là đường phân giác
nên tam giác DEF cân tại D