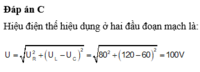Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta lấy \(U_R=1\)
\(\Rightarrow U_L=2\), \(U_C=1\)
\(\tan\varphi=\frac{U_L-U_C}{U_R}=\frac{2-1}{1}=1\)
\(\Rightarrow\varphi=\frac{\pi}{4}\)
Vậy u sớm pha hơn i là \(\frac{\pi}{4}\), hay i trễ pha với u là \(\frac{\pi}{4}\)

tan \(\varphi\)=1=\(\frac{Z_C-Z_L}{R}\Rightarrow\)ZC=R+\(\omega\)L=125
CHỌN A
Cho mình hỏi là sao phi lại bằng 1 vậy. Giải thích mình tí với

Mạch chỉ có điện trở thuần thì u cùng pha với i.
Nếu \(u=U_0\cos\left(\omega t+\varphi\right)\)
Thì: \(i=I_0\cos\left(\omega t+\varphi\right)\)
\(\Rightarrow\frac{u}{U_0}=\frac{i}{I_0}\)
\(\Rightarrow\frac{u^2}{U_0^2}+\frac{i^2}{I_0^2}=1\) là sai.

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Đáp án C.
lúc đầu ta có :
UMB=2UR => ZMB=2R <=> ZC=\(\sqrt{3}\)R mà C=\(\frac{L}{R^2}\) => ZL=\(\frac{R}{\sqrt{3}}\)
lúc sau ta có Uc' max :
Zc'.ZL=R2+ \(Z^2_L\) => Zc'=\(\frac{4R}{\sqrt{3}}\)
\(\text{tanφ}=\frac{Z_L-Z_C}{R}\Rightarrow\tan\varphi=-\sqrt{3}\Rightarrow\varphi=-\frac{\pi}{3}\)

Ta áp dụng điều kiện vuông pha với 2 đoạn mạch u1 và u2.
Khi đó: \(\tan\varphi_1.\tan\varphi_2=-1\)
\(\Leftrightarrow\frac{Z_L}{R}.\frac{Z_L-Z_C}{R}=-1\)
\(\Leftrightarrow R^2=Z_L\left(Z_C-Z_L\right)\)

Công suất tiêu thụ của mạch gồm R và r là:
\(P=I^2\left(R+r\right)\)

Mạch chỉ gồm tụ điện và điện trở nên
\(U_C=U_{AB}.\sin\alpha=50\sqrt{3}V\)
đáp án A