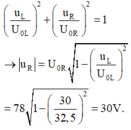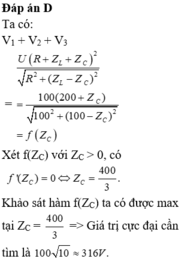
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

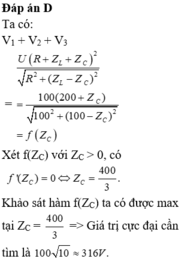

Chọn đáp án D
Ta có: Z L = ω L = 100 Ω . Đặt Z C = x
ta có: f x = U 1 + U 2 + U 3 = I Z C + Z L + R = U Z C + Z L + R R 2 + Z L − Z C 2 = 100 x + 200 100 2 + 100 − x 2
Đạo hàm f x theo x ta có: f ' = 100 100 2 + 100 − x 2 − 2 x − 200 100 x + 200 2 100 2 + 100 − x 2 100 2 + 100 − x 2
Ta có: f ' = 0 ⇔ 100 2 + 100 − x 2 − x − 100 x + 200 = 0 ⇒ x = 400 3
⇒ f = 316 , 23

Đáp án D
Có
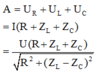
Đặt ZC = x, ta được

Để A max thì
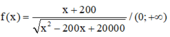
phải max
Có

Có f '=0 suy ra x=400/3. Lập bảng biến thiên tìm được Max f(x) = 3,16 khi và chỉ khi x=400/3
Suy ra MaxA=316 V

Đáp án D
Ta có:
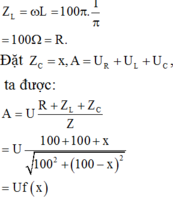
Để A đạt thì f(x) đạt cực đại. Khảo sát hàm f(x) theo x, ta có:
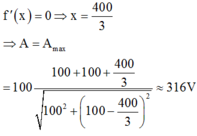

Chính là câu số 2 mình đã trả lời ở đây rùi bạn nhé: Hỏi đáp - Trao đổi kiến thức

\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)

Đáp án A
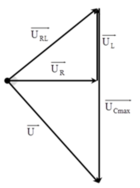
Biểu diễn vecto các điện áp.
Khi U max thì điện áp hai đầu mạch vuông pha với điện áp hai đầu đoạn mạch RL
+ Áp dụng hệ thức lượng trong tam giác, ta có:
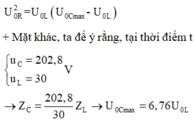
+ Thay vào phương trình hệ thức lượng ta tìm được U 0 L =32,5V
Với hai đại lượng vuông pha u L và u R ta luôn có: