Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng: \(\dfrac{2}{L_0}=\dfrac{1}{L_1}+\dfrac{1}{L_2}\)
Suy ra \(L_0=\dfrac{3}{2\pi}(H)\)

Đoạn mạch chỉ có cuộn cảm thuần thì i trễ pha \(\frac{\pi}{2}\)so với u.
\(I_0=\frac{U_0}{Z_L}=\frac{U_0}{\omega L}\)
Suy ra \(i=\frac{U_0}{\omega L}\cos\left(\omega t-\frac{\pi}{2}\right)\)

\(Z_{L1}=\omega_1.L=30\) (1)
\(Z_{C1}=\dfrac{1}{\omega_1C}=40\) (2)
Lấy (1) chia (2) vế với vế ta được: \(\omega_1^2LC=\dfrac{3}{4}\) (3)
Khi tần số \(\omega_2\) thì hệ số công suất bằng 1
\(\Rightarrow Z_{L2}=Z_{C2}\Rightarrow \omega_2.L=\dfrac{1}{\omega_2C}\)
\(\Rightarrow \omega_{2}^2LC=1\) (4)
Lấy (4) chia (3) vế với vế \(\Rightarrow \dfrac{\omega_2}{\omega_1}=\dfrac{2}{\sqrt 3}\Rightarrow \omega_2=\dfrac{2}{\sqrt 3}\omega_1\)
Chọn B.

Giải thích: Đáp án A
Phương pháp: Cường độ dòng điện hiệu dụng I = U/Z
Đoạn mạch gồm RLC mắc nối tiếp : 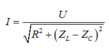 (1)
(1)
Khi nối tắt tụ : 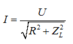
Từ (1) và (2)
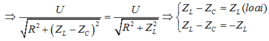
![]()

Khi C = C1 hoặc C = C2 thì I như nhau, do vậy:
\(Z_1=Z_2\Rightarrow Z_L-Z_{C1}=Z_{C2}-Z_L\Rightarrow Z_L=\dfrac{Z_{C1}+Z_{C2}}{2}=45\Omega\)
Để cường độ hiệu dụng qua R cực đại thì mạch xảy ra cộng hưởng.
\(\Rightarrow Z_C=Z_L=45\Omega\)
Chọn A.
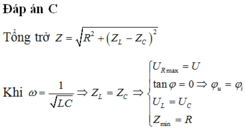

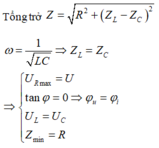

Chọn đáp án D