Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

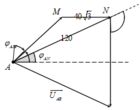
Biểu diễn vecto các điện áp. Với U A B = U A N = 120 V → AMB là tam giác cân → N A B ^ = 2 φ A N
Mặc khác khoảng thời gian ngắn nhất từ lúc điện áp hai đầu đoạn mạch AM cực đại đến lúc cường độ dòng điện trong mạch cực đại bằng khoảng thời gian ngắn nhất từ lúc điện áp hai đầu AN cực đại đến lúc điện áp u cực đại φ A M = N A B ^ = 2 φ A N
Tam giác AMN cân tại A M A N ^ = M N A ^ , ta có :
cos φ A M = cos M N A ^ = 60 40 3 = 3 2 → φ A M = 30 0 → u A N sớm pha hơn u C = u N B một góc 120 độ → Khoảng thời gian ngắn nhất từ lúc điện áp hai đầu đoạn mạch AN cực đại đến lúc điện áp hai đầu đoạn NB cực đại là là 2t
Đáp án A

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

ĐK để URC max là:
\(Zc=\frac{Z_L+\sqrt{4R^{2}+Z_L^{2}}}{2}\Rightarrow Uc=\frac{U_L+\sqrt{4Ur^{2}+U_L^{2}}}{2}=\frac{100+\sqrt{4.100^{2}.2+100^{2}}}{2}=200V\)

Bài 1:
Để công suát tiêu thụ trê mạch cực đại thì:
\((R+r)^2=(R_1+r)(R_1+r)\)
\(\Rightarrow (R+10)^2=(15+10)(39+10)\)
\(\Rightarrow R=25\Omega\)
Bài 2: Có hình vẽ không bạn? Vôn kế đo hiệu điện thế của gì vậy?

Đáp án C.
lúc đầu ta có :
UMB=2UR => ZMB=2R <=> ZC=\(\sqrt{3}\)R mà C=\(\frac{L}{R^2}\) => ZL=\(\frac{R}{\sqrt{3}}\)
lúc sau ta có Uc' max :
Zc'.ZL=R2+ \(Z^2_L\) => Zc'=\(\frac{4R}{\sqrt{3}}\)
\(\text{tanφ}=\frac{Z_L-Z_C}{R}\Rightarrow\tan\varphi=-\sqrt{3}\Rightarrow\varphi=-\frac{\pi}{3}\)