Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A'B' của một vật sáng AB đặt vuông góc với trục chính tại A của một thấu kính hội tụ có tiêu cự f = 20cm và cách thấu kính một khoảng 10cm.
A. ảnh ảo ngược chiều vật
B, ảnh ảo cùng chiều vật
C. ảnh thật cùng chiều vật
D. ảnh thật ngược chiều vật

Ảnh thật, ngược chiều và lớn hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{6}=\dfrac{1}{9}+\dfrac{1}{d'}\)
\(\Rightarrow d'=18cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{1}{h'}=\dfrac{9}{18}\Rightarrow h'=2cm\)

b)
b)
Tóm tắt:
OF = OF' = f = 12cm
OA = d = 18cm
AB = h = 10cm
A'B' = ?
OA' = ?
Giải:
\(\Delta ABF\sim\Delta OIF\)
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}\Leftrightarrow\dfrac{10}{A'B'}=\dfrac{18-12}{12}\)
\(\Rightarrow A'B'=\dfrac{10.12}{18-12}=20cm\)
\(\Delta OAB\sim\Delta OA'B'\)
\(\Rightarrow\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\Leftrightarrow\dfrac{18}{OA'}=\dfrac{10}{20}\Rightarrow OA'=\dfrac{18.20}{10}=36cm\)
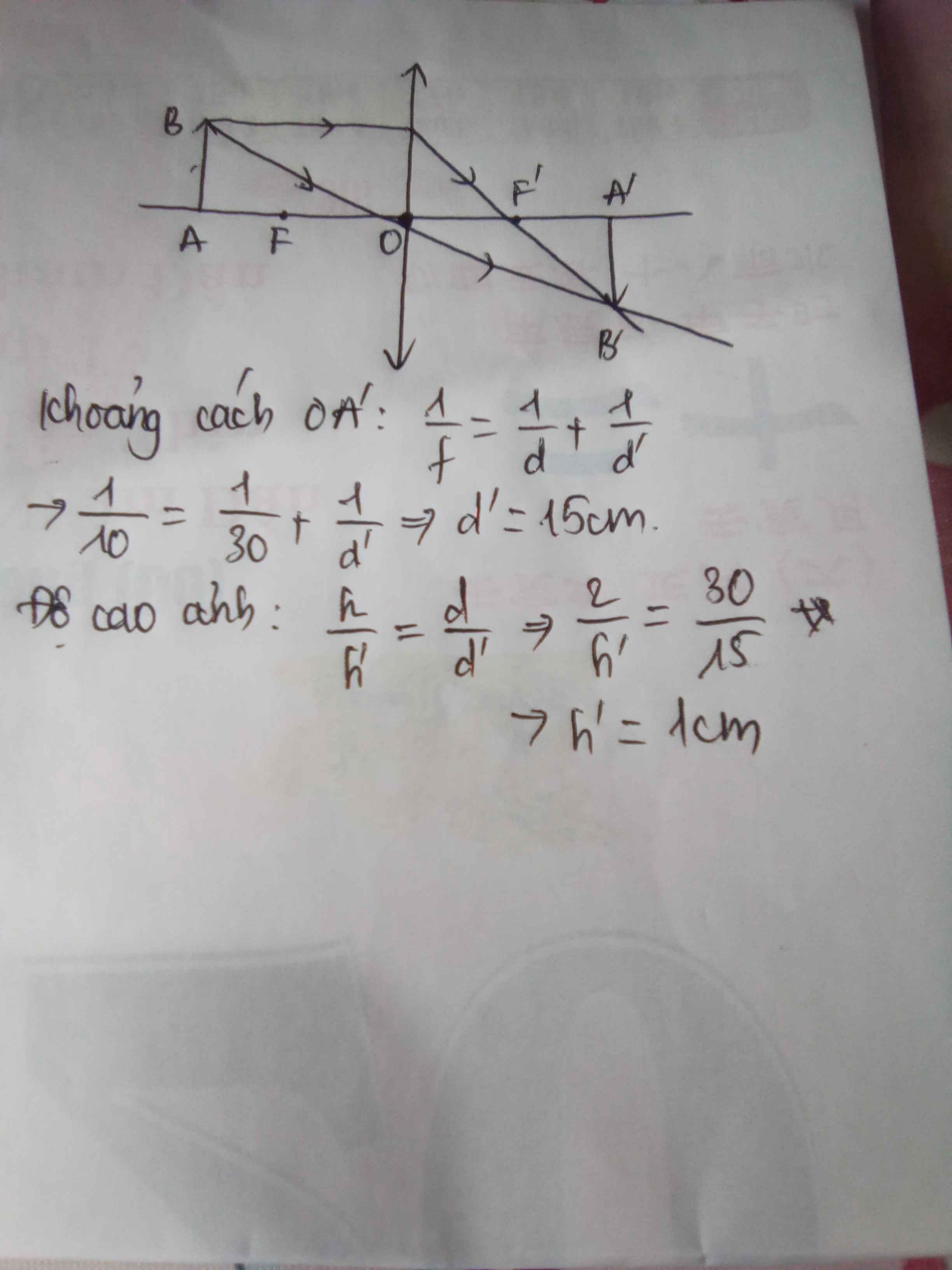
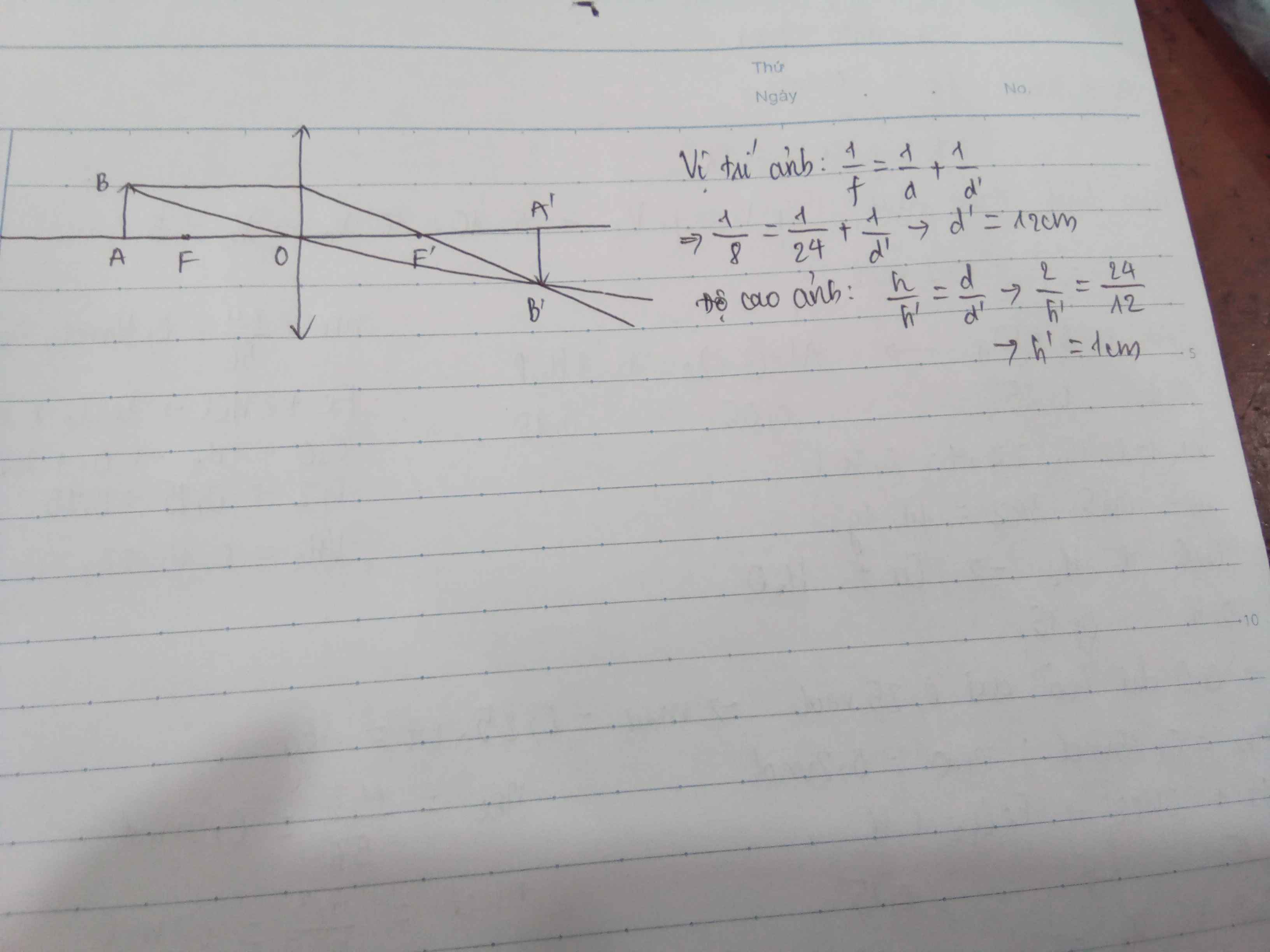

a) Chiều cao ảnh AB trước thấu kính phân kì là:
A'B' = \(\dfrac{1}{4}\)AB => AB = A'B' x 4 = 1 x 4 = 4 cm
b) Độ dài OA là:
▲A'B'O ∼ ▲ABO
=> \(\dfrac{A'B'}{AB}\) = \(\dfrac{B'O}{BO}\)
hay \(\dfrac{A'B'}{AB}\) = \(\dfrac{B'O}{BF+OF}\)
<=> \(\dfrac{1}{4}\) = \(\dfrac{5}{10+BF}\) ⇒ BF = 10 ⇒ BO = 20 cm
Xét ▲A'B'O, \(\widehat{O}\) = 90o có:
Theo định luật pytago ta có:
B'O2 + A'B'2 = OA'2 hay
252+ 12 = OA'2
⇔ OA' = \(\sqrt{26}\) cm
Tiếp đến ta có:
\(\dfrac{A'B'}{AB}\) = \(\dfrac{A'O}{AO}\) hay
\(\dfrac{1}{5}\)= \(\dfrac{\sqrt{26}}{OA}\)
⇒OA= 25,5 cm
Vậy OA = 25,5 cm
OA' = \(\sqrt{26}\) cm
AB = 4 cm