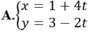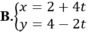Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lời giải:
Vì $(d_7)$ là đường trung trực của $AB$ nên VTPT $(d_7)$ là $\overrightarrow{AB}=(2, -2)$
$(d_7)$ đi qua đường trung điểm của $AB$ (tính chất đường trung trực) nên $(5, -2)\in (d_7)$
Vậy ptđt $(d_7)$ là:
$2(x-5)-2(y+2)=0$
$\Leftrightarrow x-5-(y+2)=0$
$\Leftrightarrow x-y-7=0$
** Lần sau bạn lưu ý, đăng đầy đủ yêu cầu của đề. Nhanh vội mà viết đề không có tâm thì khó đòi hỏi người trả lời trả lời có tâm được.
\(\overrightarrow{BA}=\left(4;3\right)\)
Gọi M là trung điểm AB \(\Rightarrow M\left(-1;\dfrac{7}{2}\right)\)
Trung trực của AB đi qua M và vuông góc AB nên nhận (4;3) là 1 vtpt
Phương trình:
\(4\left(x+1\right)+3\left(y-\dfrac{7}{2}\right)=0\Leftrightarrow4x+3y-\dfrac{13}{2}=0\)
Gọi M( 1; 3) là trung điểm của AB.
Ta có 
Gọi d là đường thẳng trung trực của AB thì d qua M( 1;3) và nhận 
làm VTCP nên có phương trình tham số là:
Chọn A.
Gọi M trung điểm của AB nên M( 2; 1)
Ta có 
Gọi d là đường thẳng trung trực của AB
thì d qua M(2; 1) và nhận 
làm VTPT.
Phương trình đường thẳng d là:
1( x- 2) – 6.(y -1) =0
Hay x- 6y+ 4= 0.
Chọn D