Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: d//d1
=>m-2=-m và m+7<>2m-3
=>m=1
b: d trùng với d2
=>m-2=-m^2 và m+7=-2m+1
=>m=-2 và m^2+m-2=0
=>m=-2
d: d vuông góc d4
=>-1/6(m+3)(m-2)=-1
=>(m+3)(m-2)=6
=>m^2+m-6-6=0
=>m^2+m-12=0
=>m=-4 hoặc m=3
c: Thay y=1/3 vào d3, ta được:
-2/3x+5/3=1/3
=>-2/3x=-4/3
=>x=2
Thay x=2 và y=1/3 vào (d), ta được:
2(m-2)+m+7=1/3
=>3m+3=1/3
=>3m=-8/3
=>m=-8/9

Hoành độ giao điểm \(d_1;d_2\)là nghiệm của phương trình \(2x-3=x-2\Rightarrow x=1\Rightarrow y=-1\Rightarrow A\left(1;-1\right)\)
Hoành độ giao điểm \(d_2;d_3\)là nghiệm của phương trình \(x-2=4x-2\Rightarrow x=0\Rightarrow y=-2\Rightarrow B\left(0;-2\right)\)
Hoành độ giao điểm \(d_1;d_3\)là nghiệm của phương trình \(2x-3=4x-2\Rightarrow x=-\frac{1}{2}\Rightarrow y=-4\Rightarrow C\left(-\frac{1}{2};-4\right)\)
Gọi \(G\left(\frac{x_A+x_B+x_C}{3};\frac{y_A+y_B+y_C}{3}\right)\)là trọng tâm tam giác ABC
Khi đó \(\frac{x_A+x_B+x_C}{3}=\frac{1+0-\frac{1}{2}}{3}=\frac{1}{6}\)
\(\frac{y_A+y_B+y_C}{3}=\frac{-1-2-4}{3}=-\frac{7}{3}\)
Vậy \(G\left(\frac{1}{6};-\frac{7}{3}\right)\)

b: Phương trình hoành độ giao điểm là:
2x+1=x-3
hay x=-4
Thay x=-4 vào y=x-3, ta được:
y=-4-3=-7

a/ \(y=-2x-5\)
\(\Rightarrow\left\{{}\begin{matrix}2m=-2\\m-1=-5\end{matrix}\right.\) \(\Rightarrow\) không tồn tại m thỏa mãn
b/ \(y=x-2\)
\(\Rightarrow2m.1=-1\Rightarrow m=-\frac{1}{2}\)
Bài 2:
Hệ phương trình tọa độ giao điểm M:
\(\left\{{}\begin{matrix}y=3x-2\\2y-x=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\) \(\Rightarrow M\left(1;1\right)\)
Bài 3:
Hệ pt tọa độ giao điểm A của d1 và d2:
\(\left\{{}\begin{matrix}y=2x-3\\y=x-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\) \(\Rightarrow A\left(2;1\right)\)
Để 3 đường thẳng đồng quy \(\Leftrightarrow d_3\) qua A
\(\Rightarrow\left(m-1\right).2+2=1\Rightarrow m=\frac{1}{2}\)

a: 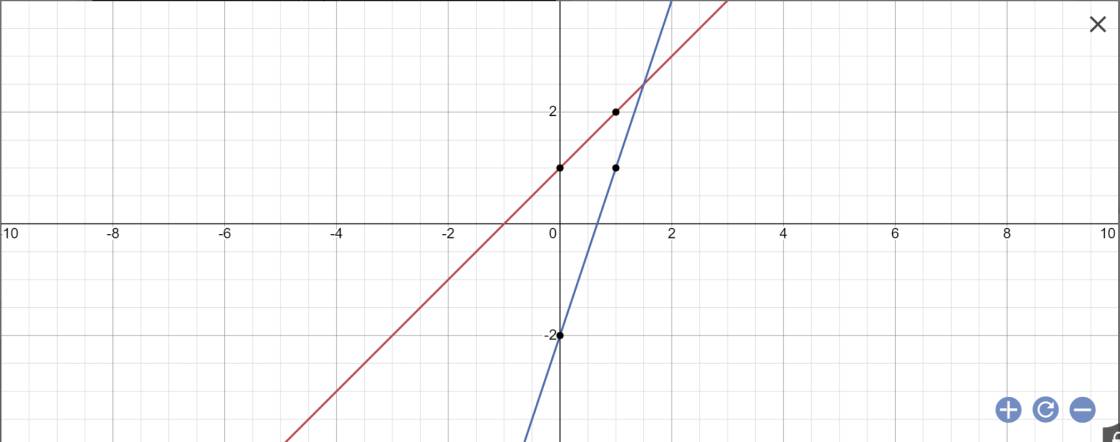
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}3x-2=x+1\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-x=2+1\\y=x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=3\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{3}{2}+1=\dfrac{5}{2}\end{matrix}\right.\)
Thay x=3/2 và y=5/2 vào (d3), ta được:
\(2m+3\cdot\dfrac{3}{2}-1=\dfrac{5}{2}\)
=>\(2m+\dfrac{7}{2}=\dfrac{5}{2}\)
=>\(2m=-1\)
=>m=-1/2
c: (d3): y=2m+3x-1
=>y=m*2+3x-1
Tọa độ điểm mà (d3) luôn đi qua là:
\(\left\{{}\begin{matrix}2=0\left(vôlý\right)\\y=3x-1\end{matrix}\right.\)
=>(d3) không đi qua cố định bất cứ điểm nào

b: Vì (d3)//(d2) nên a=-2
=>(d3): y=-2x+b
Thay x=3 vào (d1), ta được:
\(y=\dfrac{2}{3}\cdot3+2=4\)
Thay x=3 và y=4 vào (d3),ta được:
b-6=4
=>b=10
c: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}\dfrac{2}{3}x+2=-2x+1\\y=-2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{3}{8}\\y=2\cdot\dfrac{3}{8}+1=\dfrac{7}{4}\end{matrix}\right.\)

Lời giải:
Tìm tọa độ điểm $A$
PT hoành độ giao điểm $(d_1)$ và $(d_3)$:
\(x-(-x+3)=0\Leftrightarrow x=\frac{3}{2}\)
Với \(x=\frac{3}{2}\rightarrow y=\frac{3}{2}\). Vậy \(A(\frac{3}{2}; \frac{3}{2})\)
Tìm tọa độ điểm $B$:
PT hoành độ giao điểm $(d_2)$ và $(d_3)$:
\(2x-(-x+3)=0\Leftrightarrow x=1\)
Với \(x=1\rightarrow y=2x=2\). Vậy \(B(1,2)\)
\(\Rightarrow AB=\sqrt{(\frac{3}{2}-1)^2+(\frac{3}{2}-2)^2}=\frac{\sqrt{2}}{2}\)
Gọi giao điểm của $(d_3)$ với $Ox,Oy$ là $M,N$
Dễ thấy $M( 3;0); N(0; 3)$
\(\Rightarrow OM=ON=3\)
Theo hệ thức lượng trong tam giác vuông. Gọi $k$ là khoảng cách từ $O$ đến đường thẳng $AB$
\(\Rightarrow \frac{1}{k^2}=\frac{1}{OM^2}+\frac{1}{ON^2}=\frac{2}{9}\Rightarrow k=\frac{3\sqrt{2}}{2}\)
Vậy: \(S_{OAB}=\frac{k.AB}{2}=\frac{\frac{3\sqrt{2}}{2}.\frac{\sqrt{2}}{2}}{2}=\frac{3}{4}\) (đơn vị diện tích)


Tọa độ A là:
\(\left\{{}\begin{matrix}2x-2=\dfrac{1}{3}x+3\\y=2x-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{5}{3}x=5\\y=2x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5:\dfrac{5}{3}=3\\y=2\cdot3-2=6-2=4\end{matrix}\right.\)
Vậy: A(3;4)
Tọa độ B là:
\(\left\{{}\begin{matrix}-\dfrac{4}{3}x-2=\dfrac{1}{3}x+3\\y=\dfrac{1}{3}x+3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-\dfrac{5}{3}x=5\\y=\dfrac{1}{3}x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=\dfrac{1}{3}\cdot\left(-3\right)+3=3-1=2\end{matrix}\right.\)
Vậy: B(-3;2)