Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(A) Sai. Góc nội tiếp là góc có đỉnh nằm trên đường tròn, hai cạnh chứa hai dây cung của đường tròn đó.
(B) Sai. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung hoặc chắn hai cung bằng nhau.
(C) Sai. Trong một đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau.
(D) Sai. Trong một đường tròn, số đo của góc nội tiếp bằng một nửa số đo của góc ở tâm cùng chắn một cung.
(E) Đúng. Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.

a: BM là phân giác của góc ABC
=>\(\widehat{ABM}=\widehat{MBC}=\dfrac{\widehat{ABC}}{2}\)
CM là phân giác của góc ACB
=>\(\widehat{ACM}=\widehat{MCB}=\dfrac{\widehat{ACB}}{2}\)
Xét ΔMBC có \(\widehat{MBC}+\widehat{MCB}+\widehat{BMC}=180^0\)
=>\(\widehat{BMC}+\dfrac{\widehat{ABC}+\widehat{ACB}}{2}=180^0\)
=>\(\widehat{BMC}+\dfrac{180^0-\widehat{BAC}}{2}=180^0\)
=>\(\widehat{BMC}+\dfrac{180^0-a}{2}=180^0\)
=>\(\widehat{BMC}=180^0-90^0+\dfrac{a}{2}=\dfrac{a}{2}+90^0\)
Vì BM,BN lần lượt là phân giác trong và phân giác ngoài tại đỉnh B của ΔABC nên BM\(\perp\)BN
=>\(\widehat{MBN}=90^0\)
Vì CM,CN lần lượt là phân giác trong và phân giác ngoài tại đỉnh C của ΔABC nên CM\(\perp\)CN
=>\(\widehat{MCN}=90^0\)
Xét tứ giác BMCN có \(\widehat{BMC}+\widehat{BNC}+\widehat{MBN}+\widehat{MCN}=360^0\)
=>\(\widehat{BNC}+90^0+\dfrac{a}{2}+90^0+90^0=360^0\)
=>\(\widehat{BNC}=90^0-\dfrac{a}{2}\)
b: Xét tứ giác BMCN có \(\widehat{MBN}+\widehat{MCN}=90^0+90^0=180^0\)
nên BMCN là tứ giác nội tiếp đường tròn đường kính MN
=>B,M,C,N cùng thuộc đường tròn tâm O đường kính MN
Tâm O là trung điểm của MN

góc COB=40+110=150 độ
=>sđ cung nhỏ BC=150 độ
sđ cung lớn BC=360-150=210 độ
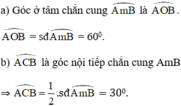


Chọn A