Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
+ Trọng lực của quả cầu: P = mg = 01.10 = 1 N
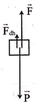
+ Ta có: P > F nên muốn quả cầu nằm cân bằng thì khi đó phải có chiều hướng lên và có độ lớn thỏa mãn:
F d h + F = P ⇒ F d h = P - F = 1 - 0.8 = 0,2 N
+ Độ giãn của lò xo tại vị trí bắt đầu thả vật: ∆ l = F d h k = 0 , 2 40 = 0 . 005 ( m ) = 0 , 5 ( c m )
+ Độ giãn của lò xo tại VTCB: ∆ l 0 = m g k = 1 40 = 0 . 025 ( m ) = 2 , 5 c m
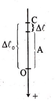
+ Từ hình bên ta có: A = = ∆ l 0 - ∆ l = 0 , 025 - 0 , 005 = 0 , 02 m
+ Lực đàn hồi cực đại tác dụng lên giá treo:
F d h m a x = k ( ∆ l 0 + A ) = 40 ( 0 , 025 + 0 , 02 ) = 1 , 8 N
+ Do ∆ l 0 > A nên lực đàn hồi cực tiểu:
F d h m i n = k ( ∆ l 0 - A ) = 40 ( 0 , 025 - 0 , 02 ) = 0 , 2 N

Kéo vật từ vị trí cân bằng xuống dưới 3cm thì thả vật ra => \(A = 3cm.\)
Hòn bi thực hiện 50 dao động toàn phần trong 20 s
=> Thời gian thực hiện 1 dao động toàn phần (chính là chu kỳ T) : \(T = \frac{20}{50} = 0,4 s.\)
\(\Delta l\) là độ dãn của lò xo khi ở vị trí cân bằng. Tại vị trí cân bằng: \(P = F_{đh}\)
=> \(mg = k\Delta l=> T = 2\pi \sqrt{\frac{m}{k}} = 2\pi\sqrt{\frac{\Delta l}{g}}.\)
=> \(\Delta l = \frac{T^2.g}{4\pi^2} = \frac{T^2}{4} = 0,04 m = 4cm.\)
Lực đàn hồi cực tiểu khác 0 => \(\Delta l \geq A\) => Lực đàn hồi cực tiểu là \(F_{đhmin}=k(\Delta l -A).\)
=> \(\frac{F_{đhmax}}{F_{đhmin}} = \frac{k(\Delta l +A)}{k(\Delta l -A)} = \frac{\Delta l +A}{\Delta l -A} = \frac{4+3}{4-3}= 7.\)

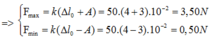
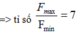
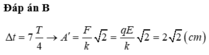




Trọng lực và lực đàn hồi ấy bạn, chắc là ban đầu đề bài cho con lắc dao động nhỏ luôn rồi ấy
D.Công Thiện Vậy câu tiếp này, vị trí cao nhất là vị trí nào?