Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi biên độ dao động là A.
Độ dãn của lò xo khi vật ở VTCB là: \(\Delta\ell_0=\dfrac{mg}{k}\)
Độ dãn cực đại của lò xo là: \(\Delta\ell_0+A=10cm=0,1m\)
Lực đàn hồi cực tiểu là: \(k(\Delta\ell_0-A)=0,8\)
\(\Rightarrow k(\Delta \ell_0+\Delta\ell_0-0,1)=0,8\)
\(\Rightarrow k(2\Delta \ell_0-0,1)=0,8\)
\(\Rightarrow k(2\dfrac{mg}{k}-0,1)=0,8\)
\(\Rightarrow2.mg-0,1.k=0,8\)
\(\Rightarrow2.0,24.10-0,1.k=0,8\)
\(\Rightarrow k=40(N/m)\)
Lực mà lò xo tác dụng lên vật khi lò xo dãn 5cm là lực đàn hồi của lò xo và bằng: \(F=k.\Delta\ell=40.0,05=2(N)\)

Tại VTCB : đental = 2.5cm
biên độ : A=(30 - 20)/2 = 5cm
vậy thời gian cần tính là t = T/4 + T/12
0k???
Bài 2 hỏi độ lớn của vật là cái j hả??????
Bai 3. oomega = 20rad/s
tại VTCB denta l = g/omega^2 = 2,5cm
A = 25 - 20 - 2,5 = 2,5cm
li độ tại vị trí lò xo có chiều dài 24cm x=24-22,5 = 1,5cm
Áp dụng CT độc lập với thời gian ta tính được v = 40cm/s
từ đó suy ra động năng thui

Hướng dẫn: Chọn đáp án A
Tại vị trí lò xo nén cực đại lần 1, tốc độ triệt tiêu và cơ năng còn lại:
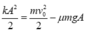
![]()

![]()

Tần số góc: \(\omega=\sqrt{\frac{K}{m}}=10\pi\left(rad\text{/}s\right)\)
Biên độ dao động của vật \(A=\sqrt{x^2+\left(\frac{v}{w}\right)^2}=6\left(cm\right)\)
Lò xo có độ nén cực đại tại biên âm:
\(\Rightarrow\) Góc quét \(=\pi\text{/}3+\pi=\omega t\Rightarrow t=2\text{/}15\left(s\right)\)
chọn B

Đáp án B
Khi chưa có lực F , vị trí cân bằng của vật là O . Biên độ là : A = 2 3 c m
Khi có thêm lực F, vị trí cân bằng dịch chuyển đến O’ sao cho : OO' = F k = 0 , 02 m = 2 c m
ω = k m = 10 π rad / s ⇒ T = 0 , 2 s
Khi F bắt đầu tác dụng (t=0), vật đến O có li độ so với O’ là : x 1 = - 2 c m và có vận tốc v 1 = ω A = 20 π 3 cm / s
Biên độ : A 1 = x 1 2 + v 1 ω 2 = 4 c m
Thời gian ngắn nhất vật đi từ O đến O’ là: t 1 = T 60 = 1 60 s
Ta thấy rằng t = 1 30 s = 2 t 1 nên khi F ngừng tác dụng thì vật có li độ so với O là x 2 = 4 c m và có vận tốc v 2 = v 1 = ω A = 20 π 3 cm / s
Từ đó biên độ từ lúc ngừng tác dụng lực là :
A 2 = x 2 2 + v 2 ω 2 = 2 7 c m
Vậy A 1 A 2 = 2 7

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)


