Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D
+ T = 1s => ω = 2π rad/s.
+ Độ biến dạng của lò xo ở vị trí cân bằng:
+ Biên độ dao động:
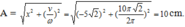
+ Thời điểm t = 0 tương ứng với một gốc lùi Δφ = ωt = 2π.2,5 = 5π trên đường tròn.
+ Lực đàn hồi khi đó có độ lớn:
Fđh = k(Δlo + x) = k(25 + 5√2). 10-2 N.
Kết hợp với Fđhmin = k.(Δlo - A) = k. 15.10-2 = 6N.
+ Từ hai biểu thức trên ta thu được Fđh = 12,82N.
Đáp án A
Theo bài ra ta có ω = π
Áp dụng hệ thức độc lập ta có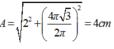 
Để xác định được pha ban đầu ta áp dụng vòng tròn lượng giác ta có
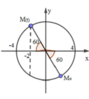
Vậy pha ban đầu là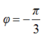 
. Phương trình dao động của vật x = 4cos(2πt - π/3) (cm)
Giải thích: Đáp án A
Phương pháp: Sử dụng lí thuyết về con lắc lò xo chịu thêm tác dụng của lực điện
Sử dụng hệ ̣thức độc lập theo thời gian của x và v
Cách giải:
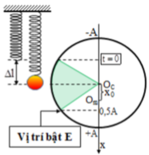
Biên độ lúc đầu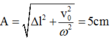 
Khi có điện trường VTCB lúc này là Om con lắc bị dịch xuống một đoạn: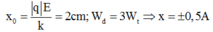 
Tại vị trí 0,5A bắt đầu thiết lập E li độ lúc này là:
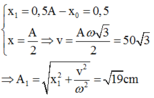
Đáp án A
+ Tần số góc của dao động: ω = k m = 60 150.10 − 3 = 20 rad/s
Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 150.10 − 3 .10 60 = 2 , 5 c m
+ Biên độ dao động ban đầu của vật: A = Δ l 0 2 + v 0 ω 2 = 2 , 5 2 + 50 3 20 2 = 5 cm.
Điện trường xuất hiện, vật đang ở vị trí động năng bằng ba lần thế năng, tại vị trí này vật có x = 0,5A = 2,5 cm, v = 3 2 ω A = 50 3 cm/s.
+ Dưới tác dung của điện trường con lắc sẽ dao động điều hòa tại vị trí cân bằng mới O′ nằm dưới vị trí cân bằng cũ một đoạn Δ l = q E k = 6.10 − 5 .2.10 4 60 = 2 cm.
→ So với vị trí cân bằng mới, tại vị thời điểm xảy ra biến cố, vật có x′ = 2,5 – 2 = 0,5 cm, v ' = 3 2 ω A = 50 3 cm/s.
Biên độ dao động mới: A ' = x ' 2 + v ' ω 2 ⇒ 0 , 5 2 + 50 3 20 2 = 19 cm.
Đáp án C
Phương pháp: Sử dụng công thức tính lực đàn hồi và trọng lượng
Cách giải:
+ Thời gian quả cầu đi từ vị trí cao nhất đến VT thấp nhất là 0,15s → T/2 = 0,15 s → T = 0,3 s.
→ Độ giãn của lò xo ở VTCB:
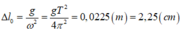
+ Khi con lắc ở vị trí thấp nhất thì: F d h = k . ( ∆ l 0 + a )
Theo đề bài ta có:
Giải thích: Đáp án B
Phương pháp: Áp dụng định luật bảo toàn động lượng, hê ̣thức độc lập với thời gian của vận tốc và li độ ̣
Cách giải:
Ở vị trí cân bằng lò xo dãn một đoạn ∆l.
Ta có k mg 0,05m 5cm
Khi quả cầu đến vị trí thấp nhất thì lò xo đang dãn đoạn: A + ∆l = 12,5 + 5 = 17,5cm và vận tốc của vật bằng 0.
Sau khi va chạm vận tốc hai vật là: mv = (m+M)v’ => 0,5.6 = 1,5.v’ => v’ = 2m/s.
Sau đó hai vật dao động điều hòa, vị trí cân bằng lò xo dãn ∆l’ với : k ' (m M)g ' 0, 075m 7,5cm
Vậy khi x = 10cm, v’ = 2m/s, 
Áp dụng công thức độc lập: 
\(x=2\sin(\omega t +\dfrac{\pi}{2})=2\cos(\omega t)\) (cm)
Như vậy, ban đầu (t = 0) vật đang ở biên độ dương \(x=2cm\)
Khi quả cầu đi được nửa chu kì dao động thì nó sẽ lên biên độ âm, \(x=-2cm\)
Chiều dài lò xo: \(\ell=\ell_0+\Delta \ell_0+x=40+10-2=48(cm)\)
Đáp án A
∆ l 01 = m g k = 2 c m
ω = k m = 10 5 rad/s
∆ l 02 = m ' g k = 2 , 5 c m
Tại VTCB sau đó , lò xo giản 2,5 cm , tại thời điểm quả cầu tới biên dưới O lò xo giản 6 cm
=> A' = (6-2,5) = 3,5 cm; ω 2 = k m ' = 20
Vị trí O ban đầu cách VTCB lúc sau 0,5 cm
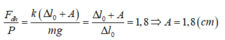
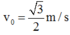
T=1s nha