Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có tỉ số E F m a x = 0 , 5 k A 2 k A = A 2 = 2 cm → A = 4 cm.

Fmax=k(Δl+A)=6 (1)
Fmin=k(Δl-A)=4 (2)
W=1/2kA^2=0,05 (3)
giải hệ 3 phương trình 3 ẩn được
Δl=5A thay vào(1) rồi lấy (3) chia (1) được A=0,1(m)=10cm

Nhớ biểu thức sau, rất hữu ích khi thi trắc nghiệm
\(W_d=n.W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{n+1}}\)
\(W_d=3W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{3+1}}=\pm\dfrac{A}{2}\)
\(\Rightarrow F_{dh}=k.\Delta l=k.\dfrac{A}{2}=\dfrac{1}{2}kA\left(N\right)\)
\(F_{dh\left(max\right)}=kA\left(N\right)\)
\(\Rightarrow\dfrac{F_{dh}}{F_{dh\left(max\right)}}=\dfrac{\dfrac{1}{2}kA}{kA}=\dfrac{1}{2}\)

Đáp án C
Phương pháp: Sử dụng lí thuyết về bài toán con lắc lò xo dao động điều hoà theo phương thẳng đứng
Cách giải:
Vật ở vị trí cân bằng thì lò xo dãn một đoạn: ∆l.
Ta có:
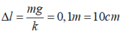
Từ vị trí cân bằng dời vật đoạn 12cm theo phương lò xo rồi buông cho dao động điều hòa => A = 12cm Vì A > ∆l nên lực đàn hồi cực tiểu tác dụng lên vật bằng 0
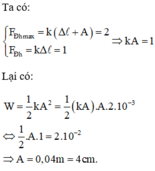



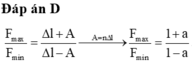
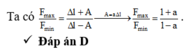
Năng lượng dao động: \(W=\dfrac{1}{2}kA^2=2.10^{-2}\) (1)
Lực đàn hồi cực đại: \(F_{dhmax}=k(\Delta \ell_0+A)=4\) (2)
Lực đàn hồi khi ở VTCB: \(F_{cb}=k.\Delta\ell_0=2\) (3)
Từ (2) và (3) suy ra: \(k.A=2\) (4)
Thế (4) vào (1) suy ra: \(A=2.10^{-2}m=2cm\)