Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Diện tích cần tính gồm diện tích xung quanh hình trụ và diện tích xung quanh hình nón.


Đáp án C.
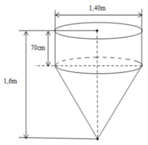
Gọi R 1 = r là bán kính đường tròn đáy của hình nón và cũng là bán kính mặt đáy của thùng.
Khi đó R 2 = 2 r là bán kính của miệng thùng và phễu, thùng có cùng chiều cao h = 20 cm.
Thể tích của thùng là V 1 = 1 3 πh R 1 2 + R 2 2 + R 1 R 2 = 1 2 . π . 20 . r 2 + 4 r 2 + r . 2 r = 140 π 3 . r 2 cm 3 .
Thẻ tích của phễu hình nón là V 2 = 1 3 πR 1 2 h = 1 3 . π . r 2 . 20 = 20 π 3 . r 2 cm 3 .
Vậy thể tích khối nước là V = V 1 - V 2 = 40 πr 2 = 4000 ⇒ r = 100 π ≈ 5 , 64 cm .

Đáp án C
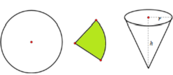
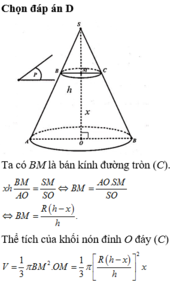
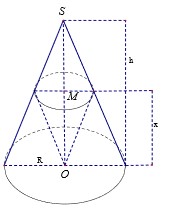
Ta có x = k . R là chu vi đường tròn đáy của khối nón ⇒ k . R = 2 π r ⇒ r = k . R 2 π
Độ dài đường sinh của khối nón chính là bán kính R ⇒ l = R = r 2 + h 2 ⇒ h = R 2 − r 2
Thể tích của khối nón là:
V = 1 3 π r 2 h = 1 3 π . r 2 . R 2 − r 2 ⇔ V 2 = π 2 9 . r 4 . R 2 − r 2 . 1
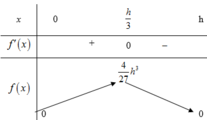
Theo bất đẳng thức Cosi, ta được r 2 . R 2 − r 2 = 4. r 2 2 . r 2 2 . R 2 − r 2 ≤ 4 R 6 27 2
Từ (1), (2) suy ra:
V = π 2 9 . 4 R 6 27 = 4 π 2 243 R 6 ⇒ V ≤ 2 π 9 3 R 3
Dấu “=” xảy ra khi:
⇔ r 2 2 = R 2 − r 2 ⇔ R 2 = 3 2 r 2 = 3 2 . k 2 R 2 4 π 2 ⇒ k 2 = 8 π 2 3 ⇒ k ≃ 5 , 13


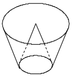
Gọi bán kính đáy của vật N1 và vật N2 lần lượt là r 1 r 2 .
Khi đó ta có:
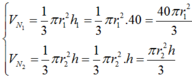
Theo đề bài ta có:
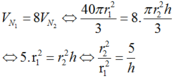
Do cắt vật N1 bằng một mặt cắt song song với mặt đáy nên theo định lý Ta-lét ta có:
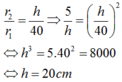
Chọn B.

Đáp án D
Ta có: 1 d 2 I ; α = 1 d 2 + 1 h 2 trong đó d là khoảng cách từ tâm của đáy đến giao tuyến của α và đáy.
Khi đó d = 15 ⇒ độ dài dây cung a = 2 r 2 − d 2 = 40 ; đường cao thiết diện = h 2 + d 2 = 25
Do đó A = 1 2 a . h ' = 1 2 .40.25 = 500 c m 2 .

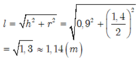

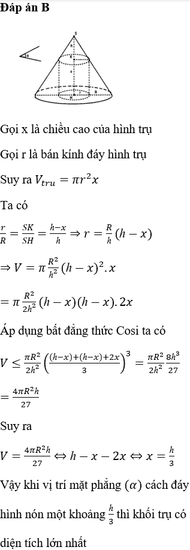
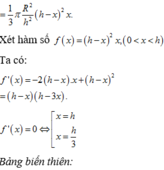
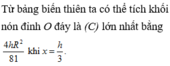
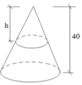

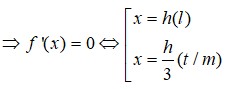

Theo đề bài ta có V = 18000 c m 3 , h = 40cm
Do đó, ta có:
V = 1 3 πr 2 h ⇒ r = 3 V πh = 3 . 18000 40 π ⇒ r ≈ 20 , 72 cm
Vậy bán kính của hình tròn là r = 21cm
Đáp án D