Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Gọi khoảng cách từ điểm M đến các mặt bên (OAB), (OBC), (OCA) lần lượt là a, b, c.
Khi đó
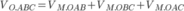
Hay 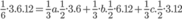

Thể tích khối gỗ hình hộp chữ nhật theo đề bài là V = abc
Ta có :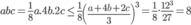 (Theo bất đẳng thức Cô-sin).
(Theo bất đẳng thức Cô-sin).
Vậy V = abc đạt giá trị lớn nhất bằng 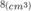 khi
khi
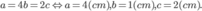
Một thửa ruộng hình chữ nhật có chiều dài 150m, chiều rộng bằng
#Hỏi cộng đồng OLM
#Mẫu giáo

Bài 1 :
giải :
Chiều rộng là
150:3x2=100[m]
Diện tích là
150x100=15000[m2]
thu hoạch được số thóc là
15000:100=150[kg]
đáp số : 150kg thóc
Bài 2:
giải
a) Thể tích bể là 4x3x2,5=30(m3)
đổi 30m3=30000 lít
Số nước có trong bể= 30000x80%=24000(l)
b) đổi 24000l=24m3
mức nc trong bể cao 24:4:3=2(m)

Người thợ đó gấp đôi mảnh vải chia thành 2 phần, sau đó tiếp tục gấp đôi manh vải của mỗi mãnh vai trên chia thành 4 phần . Bây giờ người thợ đó cắt \(\dfrac{3}{4}\) mảnh vải dựa theo 4 phần đã chia thì ta có 1 mảnh vải có diện tích 1m\(^2\).

Câu 1:
\(AB=\sqrt{\left[3-\left(-2\right)\right]^2+\left(3-2\right)^2}=\sqrt{26}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(-2-3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-2-2\right)^2}=4\sqrt{2}\)
\(P=\dfrac{AB+BC+AC}{2}=\dfrac{2\sqrt{26}+4\sqrt{2}}{2}=\sqrt{26}+2\sqrt{2}\)
\(S=\sqrt{\left(\sqrt{26}+2\sqrt{2}\right)\cdot2\sqrt{2}\cdot2\sqrt{2}\cdot\left(\sqrt{26}-2\sqrt{2}\right)}=\sqrt{18\cdot8}=12\left(đvdt\right)\)
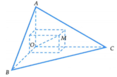
Chọn đáp án A
Gọi a, b, c lần lượt là khoảng cách từ điểm M đến các mặt phẳng (OAB),(OBC) và (OCA) (a,b,c > 0).
Ta có V O . A B C = V M . O A B + V M . O B C + V M . O C A
Thể tích của khối gỗ là
= 1 8 . 12 3 3 = 8 c m 3
Dấu “=” xảy ra khi và chỉ khi khi a =4b =2c =4