Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích hình vuông là:
\(5x5=25\left(cm^2\right)\)
Đáp số ; \(25cm^2\)

a) Xét tgiac OAI và OBI có:
+ OI chung
+ góc AOI = BOI
=> tgiac OAI = OBI (ch-gn) (1)
=> IA=IB (2 cạnh tương ứng)
=> đpcm
b) Áp dụng định lý Pitago cho tgiac AOI vuông tại A
=> OA2 = OI2 - IA2 = 100 - 36 = 64
=> OA = 8
(1) => OA = OB (2 cạnh t/ứng)
=> OB = 6cm.
c) Xét tgiac AKI và BMI có:
+ góc AIK = BIM (đối đỉnh)
+ AI = BI (từ (1))
=>> tgiac AKI = BMI (cgv-gn)
=> AK = BM (2 cạnh t/ứng)
d) Ta có OA = OB và AK = BM (cmt)
=> OA + AK = OB + BM
=> OK = OM
=> Tgiac OKM cân tại A (2)
Ta có: I thuộc OC, K thuộc Ox, M thuộc Oy
Mà OI là tia pgiac góc xOy
=> OC là tgiac góc KOM (3)
(2), (3) => OC là đường cao tgiac OKM
=> OC vuông góc MK (đpcm)
Bạn sifdksfdkjlsjlfkdjdkfsi làm tương đối đúng nhưng :
- Phần b làm ngắn vậy sẽ gây khó hiểu, mình xin phép sửa lại :
b) Xét tam giác OAI vuông tại A có :
OA2 + AI2 = OI2 (ĐL pi-ta-go)
Mà AI = 6cm (GT), OI = 10cm (GT)
=> OA2 + 62 = 102
=> OA2 + 36 = 100
=> OA2 = 100 - 36
=> OA2 = 64
=> OA2 = \(\sqrt{64}\)
=> OA = 8cm
Mà OA = OB (tương ứng)
=> OB = 8cm (đpcm)
- Phần c thì mình không nghĩ chứng minh 2 tam giác vuông mà lại có cách cm theo trường hợp cgv - gn (nếu có thật thì mình xin lỗi), thay vào đó thì cm theo g.c.g bằng 3 yếu tố : góc KAI = góc MBI = 90o, AI = BI (tương ứng), góc AIK = góc MIB (đối đỉnh).
- Phần d thì rối ghê đấy, tam giác OKM không thể nào cân tại A được, nên cm tam giác OKC = tam giác OMC rồi suy ra góc OCK = góc OCM => OC vuông góc với MK (đpcm).

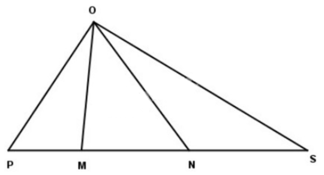
Phương pháp giải:
- Đếm các hình tam giác đơn.
- Ghép 2; 3 các hình tam giác đơn thành tam giác khác rồi đếm cho đến hết.
Lời giải chi tiết:
Chọn D. 6 hình tam giác.
Các hình tam giác là: OPM, OMN, ONS, OPN, OMS, OPS.

dien tich cua hionh tam giac la :
4/3x5/4=5/6
dap so 5/6

Diện tích tờ giấy hình chữ nhật ban đầu là: 15 x 8= 120 (cm2)
Diện tích hình vuông là: 120-84=36(cm2)
Cạnh hình vuông là: 36:4=9(cm)
Đ/s: 9 cm

Có 2 gọc vuông 2 góc không vuông