Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ \(F_{hd}=G.\frac{m_1.m_2}{r^2}=G.\frac{6.10^{24}.72.10^{21}}{38.10^7}=...\) (số kinh dị quá cậu tự tính nha) >_<
2/ Lực hấp dãn đặt vào 1 vật triệt tiêu tức là lực hấp dẫn 2 hành tinh t/d lên vật đó là như nhau
\(F_{hd1}=G\frac{m_{TĐ}.m_v}{r_1^2}\)
\(F_{hd2}=G\frac{m_v.m_t}{r_2^2}=G.\frac{m_v.m_t}{\left(38.10^7-r_1\right)^2}\)
\(\Leftrightarrow\frac{m_{TĐ}}{r_1^2}=\frac{m_t}{\left(38.10^7-r_1\right)^2}\)
thay mTĐ và mt vào tìm đc r1

Đáp án C
Gọi x là khoảng cách từ vật thứ nhất đến vị trí tại mà tại đó lực hấp dẫn do hai vật tác dụng lên vật m3 bất kỳ bằng 0
![]()
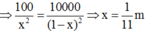

Chọn đáp án A
+ Theo điều kiện cân bằng 
Vậy m 3 phải đặt trong khoảng hai vật và đặt trên đường thẳng nối hai vật
Gọi x là khoảng cách từ vật m 1 đến m 3 thì khoảng cách từ m 2 đến m 3 là 0,2 – x
Ta có
![]()
![]()
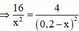
![]()
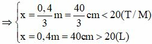
Vậy m 3 cách m 1 40/3cm và cách m 2 là 20/3cm

Theo điều kiện cân bằng F 13 → + F 23 → = 0 ⇒ F 13 → ↑ ↓ F 23 → F 13 = F 23
Vậy m3 phải đặt trong khoảng hai vật và đặt trên đường thẳng nối hai vật
Gọi x là khoảng cách từ vật m 1 đến m 3 thì khoảng cách từ m 2 đến m 3 là 0,2 – x
F 13 = F 23 ⇒ G m 1 m 3 x 2 = G m 2 m 3 ( 0 , 2 − x ) 2 ⇒ m 1 x 2 = m 2 ( 0 , 2 − x ) 2
⇒ 16 x 2 = 4 ( 0 , 2 − x ) 2 ⇒ 4 ( 0 , 2 − x ) 2 = x 2 ⇒ 2 ( 0 , 2 − x ) = x 2 ( 0 , 2 − x ) = − x
⇒ x = 0 , 4 3 m = 40 3 c m < 20 ( T / M ) x = 0 , 4 m = 40 c m > 20 ( L )

gọi khoảng cách từ m đến m1 là x
khoảng cách từ m đến m2 là 0,1-x
\(F_{hd1}=F_{hd2}\) và m1=9m2
\(\Rightarrow\)\(\dfrac{G.m.m_1}{x^2}=\dfrac{G.m.m_2}{\left(0,1-x\right)^2}\)\(\Rightarrow x=0,075\)m
vậy m cách m1 một khoảng x=0,075m

\(\overrightarrow{F_D}+\overrightarrow{F_A}+\overrightarrow{F_B}=\overrightarrow{0}\Leftrightarrow F_D^2=F_A^2+F_B^2\)
\(\Leftrightarrow\left(\dfrac{G.m'.m\sqrt{2}}{AD^2}\right)^2=\left(\dfrac{G.m.m'}{AB^2}\right)^2+\left(\dfrac{G.m'.m}{AC^2}\right)^2\)
\(\Leftrightarrow\left(\dfrac{\sqrt{2}}{AD^2}\right)^2=\dfrac{1}{AB^4}+\dfrac{1}{AC^4}\Leftrightarrow\dfrac{2}{AD^2}=\dfrac{1}{a^4}+\dfrac{1}{a^4}=\dfrac{2}{a^4}\)
\(\Rightarrow AD=a^2\)
\(\overrightarrow{F_D}+\overrightarrow{F_A}+\overrightarrow{F_B}=\overrightarrow{0}\Leftrightarrow F_D^2=F_A^2+F_B^2\)
\(\Leftrightarrow\left(\dfrac{G.m'.m\sqrt{2}}{AD^2}\right)^2=\left(\dfrac{G.m.m'}{AB^2}\right)^2+\left(\dfrac{G.m'.m}{AC^2}\right)^2\)
\(\Leftrightarrow\left(\dfrac{\sqrt{2}}{AD^2}\right)^2=\dfrac{1}{AB^4}+\dfrac{1}{AC^4}\Leftrightarrow\dfrac{2}{AD^2}=\dfrac{1}{a^4}+\dfrac{1}{a^4}=\dfrac{2}{a^4}\)
\(\Rightarrow AD=a^2\)

\(F_{hd}=\dfrac{Gm_1m_2}{r^2}=1,334.10^{-7}\)
\(F_{hd}'=\dfrac{Gm_1m_2}{r'^2}=\dfrac{Gm_1m_2}{\left(r-5\right)^2}=5,336.10^{-7}\)
\(\Rightarrow\dfrac{F_{hd}}{F_{hd}'}=\dfrac{\left(r-5\right)^2}{r^2}=\dfrac{1334}{5336}\Rightarrow r=...\left(m\right)\)
\(\Rightarrow m_1m_2=\dfrac{5,336.10^{-7}.\left(r-5\right)^2}{G}=...\)
\(\left\{{}\begin{matrix}m_1m_2=...\\m_1+m_2=900\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m_1=...\left(kg\right)\\m_2=...\left(kg\right)\end{matrix}\right.\)
Hằng số G có trong SGK, bạn tự tìm