Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B M B' M' d
Từ A hạ \(AB'\perp d\). (B' thuộc d).
Trên AB' lấy điểm M sao cho AM' = 2M'B. Điểm A và d cố định nên M' và B' cố định.
Áp dụng định lý Ta-let: \(\dfrac{AM'}{AB'}=\dfrac{AM}{MB}=2\).
Suy ra M'M // B'B hay M'M // d.
Vậy điểm M thuộc đường thẳng đi qua M' và song song với d.

A B C D E F M I S
a) Dễ thấy: \(\Delta\)BME vuông cân tại E => BE = ME (1)
Xét tứ giác AEMF: ^FAE = ^AEM = ^AFM = 900 => Tứ giác AEMF là hình chữ nhật => ME = AF (2)
(1); (2) => BE = AF => \(\Delta\)CBE = \(\Delta\)BAF (c.g.c) => CE = BF (đpcm)
Đồng thời: ^BCE= ^ABF. Mà ^ABF + ^CBF = 900
Nên ^BCE + ^CBF = 900 hay ^BCI + ^CBI = 900 => CE vuông góc BF tại I => ^EBF = ^MEC (Cùng phụ ^BEC)
Xét \(\Delta\)BEF và \(\Delta\)EMC có: ^EBF = ^MEC; BE = EM; BF = EC => \(\Delta\)BEF = \(\Delta\)EMC (c.g.c)
=> EF = MC (2 canh tương ứng) (đpcm).
b) Gọi S là trung điểm cạnh BC
Xét \(\Delta\)BIC: Vuông tại I; trung tuyến IS => IS = BC/2 = a/2
=> I luôn cách S 1 khoảng không đổi bằng a/2. Ta có: S là trung điểm cạnh BC nên S cố định => ĐPCM.
c) C/m tương tự câu a: DE vuông góc CF
Do CE vuông góc BF (cmt) nên ^EIF = 900 => ^IFE + ^IEF = 900 hay ^CEF + ^BFE = 900
Mà \(\Delta\)BEF = \(\Delta\)EMC (cmt) => ^BFE = ^ECM (2 góc tương ứng)
Nên ^CEF + ^ECM = 900 => CM vuông góc EF
Xét \(\Delta\)EFC: DE vuông góc CF; BF vuông góc CE; CM vuông góc EF
=> BF; CM; DE đồng qui (đpcm).

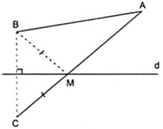
Vẽ điểm C đối xứng với B qua đường thẳng d, giả sử tìm được điểm M trên d thì MB = MC ( 1 ).
Do A, B, d cố định nên C cũng cố định suy ra độ dài đoạn AC không đổi.
Áp dụng bất đẳng thức tam giác ta có vào Δ AMC ta được: MA + MC ≥ AC ( 2 )
Dấu bằng xảy ra khi M nằm giữa A và C hay M là giao điểm của AC và đường thẳng d
Từ ( 1 ) và ( 2 ) suy ra MA + MB nhỏ nhất bằng AC khi M là giao điểm của AC và đường thẳng d

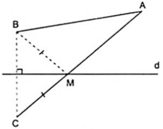
Vẽ điểm C đối xứng với B qua đường thẳng d, giả sử tìm được điểm M trên d thì MB = MC ( 1 ).
Do A, B, d cố định nên C cũng cố định suy ra độ dài đoạn AC không đổi.
Áp dụng bất đẳng thức tam giác ta có vào Δ AMC ta được: MA + MC ≥ AC ( 2 )
Dấu bằng xảy ra khi M nằm giữa A và C hay M là giao điểm của AC và đường thẳng d
Từ ( 1 ) và ( 2 ) suy ra MA + MB nhỏ nhất bằng AC khi M là giao điểm của AC và đường thẳng d