Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(y'=6x^2+6\left(m-1\right)x+6\left(m-2\right)=6\left(x+1\right)\left(x+m-2\right)\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-m+2\end{matrix}\right.\)
Phương trình nghịch biến trên đoạn có độ dài lớn hơn 3 khi:
\(\left|-1-\left(-m+2\right)\right|>3\)
\(\Leftrightarrow\left|m-3\right|>3\Rightarrow\left[{}\begin{matrix}m>6\\m< 0\end{matrix}\right.\)
2.
\(y'=-3x^2+6x+m-1\)
\(\Delta'=9+3\left(m-1\right)>0\Rightarrow m>-2\)
Gọi \(x_1;x_2\) là 1 nghiệm của pt \(-3x^2+6x+m-1=0\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=\dfrac{-m+1}{3}\end{matrix}\right.\)
Hàm đồng biến trên đoạn có độ dài lớn hơn 1 khi:
\(\left|x_1-x_2\right|>1\)
\(\Leftrightarrow\left(x_1-x_2\right)^2>1\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2>1\)
\(\Leftrightarrow4-\dfrac{-4m+4}{3}>1\)
\(\Rightarrow m>-\dfrac{5}{4}\) \(\Rightarrow m=-1\)
Có đúng 1 giá trị nguyên âm của m thỏa mãn
3.
\(y'=x^2+6\left(m-1\right)x+9\)
\(\Delta'=9\left(m-1\right)^2-9>0\Rightarrow\left[{}\begin{matrix}m>1\\m< 0\end{matrix}\right.\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-6\left(m-1\right)\\x_1x_2=9\end{matrix}\right.\)
\(\left|x_1-x_2\right|=6\sqrt{3}\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=108\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=108\)
\(\Leftrightarrow36\left(m-1\right)^2-36=108\)
\(\Rightarrow\left(m-1\right)^2=4\Rightarrow\left[{}\begin{matrix}m=3\\m=-1\end{matrix}\right.\)
Có 1 giá trị nguyên âm của m thỏa mãn

31.
\(y'=\dfrac{1+m}{\left(x+1\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi:
\(\dfrac{1+m}{\left(x+1\right)^2}>0\Rightarrow m>-1\) (C)
32.
\(y'=\dfrac{4-m^2}{\left(x+4\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi:
\(4-m^2>0\Rightarrow-2< m< 2\)
\(\Rightarrow m=\left\{-1;0;1\right\}\)
Có 3 giá trị nguyên của m
33.
\(y'=\dfrac{m-1}{\left(x+1\right)^2}\)
Hàm đồng biến trên từng khoảng xác định khi:
\(m-1>0\Rightarrow m>1\)
34.
\(y'=\dfrac{2m-1}{\left(x+2m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}2m-1>0\\-2m>-3\end{matrix}\right.\) \(\Rightarrow\dfrac{1}{2}< m< \dfrac{3}{2}\)
\(\Rightarrow m=1\)
Có 1 giá trị nguyên của m

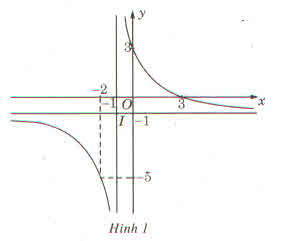
a) (H) có các đường tiệm cận là:
- Tiệm cận ngang y = -1
- Tiệm cận đứng x = -1
hai đường tiềm cận này cắt nhau tại điểm I(-1; -1).
Hình (H') có hai đường tiệm cận cắt nhau tại I'(2;2) nên ta cần phép tịnh tiến theo vector \(\overrightarrow{II'}=\left(2-\left(-1\right);2-\left(-1\right)\right)=\left(3;3\right)\)
b) Hình (H') có phương trình là:
\(y+3=\dfrac{3-\left(x+3\right)}{\left(x+3\right)+1}\) hay là \(y=\dfrac{-4x-12}{x+4}\)
Hình đối xứng với (H') qua gốc tọa độ có phương trình là:
\(-y=\dfrac{-4\left(-x\right)-12}{-x+4}\) hay là: \(y=\dfrac{4x-12}{-x+4}\)

Giả sử z = x + yi (x, y ∈ R), khi đó số phức z được biểu diễn bởi điểm M(x, y) trên mặt phẳng tọa độ Oxy.
a) Trên hình 71.a (SGK), điểm biểu diễn ở phần gạch chéo có hoành độ có hoành độ x ≥ 1, tung độ y tùy ý.
Vậy số phức có phần thực lớn hơn hoặc bằng -1 có điểm biểu diễn ở hình 71.a (SGK)
b) Trên hình 71.b(SGK), điểm biểu diễn có tung độ y ∈ [1, 2], hoành độ x tùy ý.
Vậy số phức có phần ảo thuộc đoạn [-1, 2]
c) Trên hình 71.c (SGK), hình biểu diễn z có hoành độ x ∈ [-1, 1] và x2 + y2 ≤ 4 (vì |z| ≤ 4.
Vậy số phực có phần thực thuộc đoạn [-1, 1] và môdun không vượt quá 2.

8.
Hàm có 1 điểm cực đại \(\left(x=-1\right)\)
9.
Hàm có 1 điểm cực tiểu (\(x=-1\))
14.
\(y'=\dfrac{2x\left(x+1\right)-\left(x^2+3\right)}{\left(x+1\right)^2}=\dfrac{x^2+2x-3}{\left(x+1\right)^2}\)
\(y'=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Xét dấu y' trên trục số:
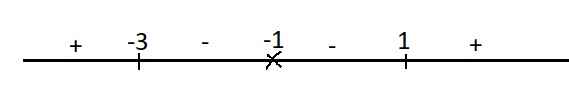
Từ dấu của y' ta thấy \(x=1\) là điểm cực tiểu
\(\Rightarrow y_{CT}=y\left(1\right)=2\)

Lời giải:
PT hoành độ giao điểm:
\(mx+2m+1-\frac{2x+1}{x+1}=0\Leftrightarrow mx^2+x(3m-1)+2m=0\)
Để hai ĐTHS cắt nhau tại hai điểm $A,B$ thì \(m\neq 0\) và:
\(\Delta=(3m-1)^2-8m^2=m^2-6m+1>0\)
Khi đó áp dụng hệ thức Viete có \(\left\{\begin{matrix} x_1+x_2=\frac{1-3m}{m}\\ x_1x_2=2\end{matrix}\right.\)
Ta có:
\(d(A,Ox)=d(B,Ox)\Leftrightarrow |mx_1+2m+1|=|mx_2+2m+1|\)
TH1: \(mx_1+2m+1=mx_2+2m+1\Leftrightarrow x_1=x_2\)
\(\Rightarrow x_1=x_2=\sqrt{2}\Rightarrow \frac{1-3m}{m}=2\sqrt{2}\) kéo theo \(m=\frac{1}{2\sqrt{2}+3}\) (không thỏa mãn đk của \(\Delta)\)
TH2: \(mx_1+2m+1=-(mx_2+2m+1)\Leftrightarrow m(x_1+x_2)+4m+2=0\)
\(\Leftrightarrow 3+m=0\Rightarrow m=-3\) (t/m)
Vậy $m=-3$

Lời giải:
Vì \(\frac{a}{b}\) chưa tối giản nên tồn tại một số \(d\in\mathbb{N}>1\) sao cho \(a\vdots d,b\vdots d\)
Khi đó \(a-b\vdots d\)
a)
Thấy $a$ và $a-b$ đều chia hết cho $d$ nên \(\frac{a}{a-b}\) không phải phân số tối giản
b) Vì \(a\vdots d\) và \(b\vdots d\) nên \(2a,2b\vdots d\). Do đó \(a-2b\vdots d\)
Thấy $2a$ và $a-2b$ đều chia hết cho $d$ nên \(\frac{2a}{a-2b}\) không phải phân số tối giản.
Ta có đpcm.
P/s: Phiền bạn từng sau đăng bài nên chú ý đăng đúng box. Bài này nên đăng ở box toán 6 thôi nhé.








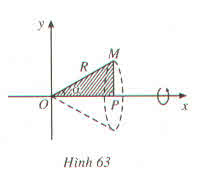
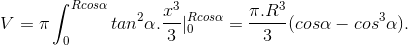
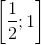 . (vì α ∈
. (vì α ∈ 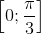 ), α = arccos t.
), α = arccos t.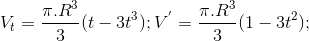
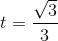
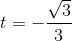 (loại).
(loại).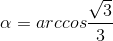 .
.
Vì \(f\left(b\right)\) đồng biến nên nếu \(f\left(-8\right)>0\Rightarrow f\left(b\right)>0;\forall b>-8\)
\(\Rightarrow f\left(b\right)\le0\) có nhiều nhất 3 nghiệm nguyên thuộc (-12;12) là -11;-10;-9 (ktm yêu cầu đề bài)
Do đó \(f\left(-8\right)\le0\)
Hiểu đơn giản thì đếm từ -11 trở đi thêm 4 số nguyên ta sẽ chạm tới mốc -8
Con vẫn không hiểu lắm ạ, nếu đếm từ 11 trở lui có được không ạ?