TT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
15 tháng 10 2018
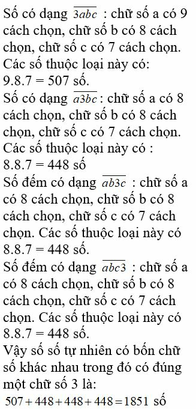
Số có dạng 3 a b c : chữ số a có 9 cách chọn, chữ số b có 8 cách chọn, chữ số c có 7 cách chọn. Các số thuộc loại này có: 9.8.7 = 507 số.
Số có dạng a 3 b c : chữ số a có 8 cách chọn, chữ số b có 8 cách chọn, chữ số c có 7 cách chọn. Các số thuộc loại này có : 8.8.7 = 448 số
Số đếm có dạng a b 3 c : chữ số a có 8 cách chọn, chữ số b có 8 cách chọn, chữ số c có 7 cách chọn. Các số thuộc loại này có 8.8.7 = 448 số.
Số đếm có dạng a b c 3 : chữ số a có 8 cách chọn, chữ số b có 8 cách chọn, chữ số c có 7 cách chọn. Các số thuộc loại này có 8.8.7 = 448 số.
Vậy số số tự nhiên có bốn chữ số khác nhau trong đó có đúng một chữ số 3 là: 507 + 448 + 448 +448 = 1851 số
Nhận xét: Bài toán yêu cầu có duy nhất (đúng một) số 3, các chữ số chỉ lặp lại có đúng 1 lần vì vậy khi giải toán cần đọc kỹ yêu cầu đề toán.
4 tháng 8 2015
Bài 14:
a) Số chứa ít nhất 1 chữ số 1 thì số đó có thể chứa 1 chữ số 1 hoặc chứa 2 chữ số 1 hoặc số đó chứa tất cả các chữ số 1
- Có 900 số có 3 chữ số
- Tìm các số có 3 chữ số đều khác chữ số 1 => số đó chỉ được tạo thành từ các chữ số 0;2;3;..;9
Chữ số hàng trăm có 8 cách chọn (trừ đi chữ số 0 và 1)
Chữ số hàng chục có 9 cách chọn (trừ đi chữ số 1 ); chữ số hàng đơn vị cũng có 9 cách chọn
=> có 8.9.9 = 648 số có 3 chữ số đều khác 1
=> Số có 3 chữ số chứa ít nhất 1 chữ số 1 = Số các số có 3 chữ số - Số các số có 3 chữ số đều khác chữ sô 1 = 900 - 648 =252 số
b) Tương tự phần a:
- Có 9000 số có 4 chữ số
- Tìm các số có 4 chữ số đều khác chữ số 1
Chữ số hàng nghìn có 8 cách chọn; chữ số hàng trăm;chục , đơn vị đều có 9 cách chọn
=> Có 8.9.9.9 = 5832 số
=> Số các số có 4 chữ số chứa ít nhất 1 chữ số 1 = Số các số có 4 chữ số - Số các số có 4 chữ số đều khác chữ số 1 = 9000 - 5832 = 3168 số
21 tháng 7 2017
1) Co 9 cach chon chu so hang tram => Co 81 so
Co 8 cach chon chu so hang chuc => Co 72 so
Co 8 cach chon chu so hang don vi => Co 72 so
Vay co tong cong 81 + 72 + 72 = 225 so
24 tháng 8 2017
Đặt y = x2 – 1 suy ra y2 = x4 – 2x2 + 1
Biến đổi P(x) = 2(x4 – 2x2 + 1) + 3x3 – 5x2 – 3x
= 2(x2 – 1)2 + 3x( x2 – 1) – 5x
Từ đó Q(y) = 2y2 + 3xy – 5x2
Tìm m, n sao cho m.n = - 10x2 và m + n = 3x chọn m = 5x , n = - 2x
Ta có: Q(y) = 2y2 + 3xy – 5x2
= 2y2 – 2xy + 5xy – 5x2
= 2y(y – x) + 5x(y – x)
= ( y – x)( 2y – 5x)
Do đó: P(x) = (x2 – x – 1 )(2x2 + 5x – 2).
24 tháng 8 2017
Đặt y = x2 – 1 suy ra y2 = x4 – 2x2 + 1
Biến đổi P(x) = 2(x4 – 2x2 + 1) + 3x3 – 5x2 – 3x
= 2(x2 – 1)2 + 3x( x2 – 1) – 5x
Từ đó Q(y) = 2y2 + 3xy – 5x2
Tìm m, n sao cho m.n = - 10x2 và m + n = 3x chọn m = 5x , n = - 2x
Ta có: Q(y) = 2y2 + 3xy – 5x2
= 2y2 – 2xy + 5xy – 5x2
= 2y(y – x) + 5x(y – x)
= ( y – x)( 2y – 5x)
Do đó: P(x) = (x2 – x – 1 )(2x2 + 5x – 2).