Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi phân số tối giản phải tìm là a/b; (a; b ∈ Z; b ≠ 1), ƯCLN (a, b) = 1
Ta có a.b = 3150 = 2. 32. 52. 7 và a, b đều là ước của 3150.
Vì phân số này có thể viết được dưới dạng số thập phân hữu hạn nên b chỉ có ước nguyên tố là 2 và 5.
Do đó, b ∈ {2; 25; 50}.
- Với b = 2 thì a = 3150:2 = 1575
- Với b = 25 thì a = 3150:25 = 126
- Với b = 50 thì a = 3150:50 = 63
Vậy các phân số phải tìm là:
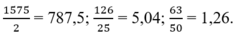
Ta viết các phân số dưới dạng phân số tối giản:
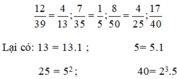
Suy ra: phân số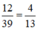 
viết được số thập phân vô hạn tuần hoàn.
Chọn (A). 12/39
Vì mẫu của các phân số này khi phân tích thành thừa số nguyên tố có thừa số khác 2 và 5 nên các phân số này đều viết được dưới dạng số thập phân vô hạn tuần hoàn
phân số thập phân là phân số có mẫu là 10; 100; 1000; ...
phân số thập phân này có tích tử và mẫu là 260 vậy, tử và mẫu lần lượt là 26 và 10
phân số có dạng \(\frac{26}{10}\) tối giản đi được \(\frac{13}{5}\)
đáp số là \(\frac{13}{5}\) nhá bạn, mình ko nhớ kiến thức cơ bản nên cũng phải học lại cái đó mới ra dc bài này, phân số thập phân học từ lp 5 rồi nhá
Gọi 3 phân số đó là \(\frac{a}{x},\frac{b}{y},\frac{c}{z}\)
Ta có các tử tỉ lệ với 3;4;5=>a:b:c=3:4:5=>\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)
Đặt \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=k\)
=>\(\hept{\begin{cases}a=3k\\b=4k\\c=5k\end{cases}}\)
Lại có các mẫu tỉ lệ với 5,1,2=>x:y:z=5:1:2=>\(\frac{x}{5}=\frac{y}{1}=\frac{z}{2}\)
Đặt \(\frac{x}{5}=\frac{y}{1}=\frac{z}{2}=h\)
=> \(\hept{\begin{cases}x=5h\\y=h\\z=2h\end{cases}}\)
Ta có tổng 3 phân số là \(\frac{213}{70}\)
=> \(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=\frac{213}{70}\)
(=) \(\frac{3k}{5h}+\frac{4k}{h}+\frac{5k}{2h}=\frac{213}{70}\)
(=) \(\frac{k}{h}.\left(\frac{3}{5}+4+\frac{5}{2}\right)=\frac{213}{70}\)
(=) \(\frac{k}{h}=\frac{3}{7}\)
=> \(\hept{\begin{cases}\frac{a}{x}=\frac{9}{35}\\\frac{b}{y}=\frac{12}{7}\\\frac{c}{z}=\frac{15}{14}\end{cases}}\)
bài 3
Ta có \(\frac{3a-2b}{5}=\frac{2c-5a}{3}=\frac{5b-3c}{2}\)
= \(\frac{15a-10b}{25}=\frac{6c-15a}{9}=\frac{10b-6a}{4}\)
=\(\frac{15a-10b+6c-15a+10b-6a}{25+9+4}=0\)
=> \(\hept{\begin{cases}3a-2b=0\\2c-5a=0\\5b-3c=0\end{cases}\left(=\right)\hept{\begin{cases}3a=2b\\2c=5a\\5b=3c\end{cases}\left(=\right)\hept{\begin{cases}\frac{a}{2}=\frac{b}{3}\\\frac{c}{5}=\frac{a}{2}\\\frac{b}{3}=\frac{c}{5}\end{cases}}}}\)
=> \(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}=\frac{a+b+c}{2+3+5}=\frac{-50}{10}=-5\)
=> \(\hept{\begin{cases}a=-10\\b=-15\\c=-25\end{cases}}\)
cho mình sửa đề bài. viết đc dưới dạng stp hữu hạn nha