Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
+ Xét hàm số f( x) = x3- x2+ ( m2+ 1) x- 4m- 7 trên đoạn [ 0; 2]
Ta có f’ (x) = 3x2- 2x+ m2+ 1= 3( x-1/3) 2+ m2+ 2/3> 0 .
+ Suy ra hàm số f(x) đồng biến trên
0 ; 2 ⇒ m i n [ 0 ; 2 ] f ( x ) = f ( 0 ) = - 4 m - 7 m a x [ 0 ; 2 ] f ( x ) = f ( 2 ) = 2 m 2 - 4 m - 1
+ Khi đó
m a x [ 0 ; 2 ] y = m a x [ 0 ; 2 ] f ( x ) = m a x - 4 m - 7 ; 2 m 2 - 4 m - 1 ≤ 15 ⇔ - 4 m - 7 ≤ 15 2 m 2 - 4 m - 1 ≤ 15 ⇔ - 11 2 ≤ m ≤ 2 2 m 2 - 4 m - 16 ≤ 0 ⇔ - 11 2 ≤ m ≤ 2 - 2 ≤ m ≤ 4 ⇔ - 2 ≤ m ≤ 2 → m ∈ ℤ m ∈ ± 2 ; ± 1 ; 0
Vậy có 5 giá trị thoả mãn.
Chọn C.
Đáp án C
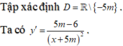
Để hàm số nghịch biến trên khoảng ( 10 ; + ∞ ) thì
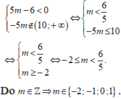
Chọn C
Hàm số f(x) =
2
x
2
+
m
x
+
2
3
2
xác định với mọi
x
∈
ℝ
Vì m nguyên nên 
Vậy có tất cả 7 giá trị m thỏa mãn điều kiện đề bài.
* Nếu m = 0 thì y = x nên hàm số đã cho không có tiệm cận ngang.
* Nếu m = 1 thì y = 1 nên hàm số không có tiệm cận ngang.
* Nếu m = -1 thì y = -1 nên hàm số không có tiệm cận ngang.
Vậy để hàm số đã cho có tiệm cận ngang thì m ≠ 0 và m ≠ ±1;
Chọn D
Chọn A
Hàm số f(x) = (x-6) x 2 + 4 xác định và liên tục trên đoạn [0;3].
Suy ra 
với a là số nguyên và b, c là các số nguyên dương nên
a = - 12, b = 3, c = 13. Do đó: S = a + b + c = 4.
Lời giải:
Xét thấy bậc của hàm số trên tử nhỏ hơn bậc của hàm số dưới mẫu, do đó đồ thị hàm số luôn có 1 TCN \(y=0\)
Khi đó, để ĐTHS có 3 đường tiệm cận thì nó phải có thêm 2 TCĐ
Thấy \(x^3+mx^2=x^2(x+m)\). Để có 2 TCĐ thì trước tiên phương trình trên phải có 2 nghiệm phân biệt, do đó \(m\neq 0\)
Khi đó, PT có hai nghiệm \(x=0,x=-m\). Để tồn tại hai nghiệm này thì :\(\left\{\begin{matrix} 0^2-3m+2\neq 0\\ (-m)^2-3m+2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq \frac{2}{3}\\ (m-1)(m-2)\neq 0\Leftrightarrow m\neq 1,2\end{matrix}\right.\)
Từ những điều trên suy ra \(m\in \left\{3;4;5\right\}\)