Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Để hàm số bậc bốn y = x 4 + b x 2 + c có 3 cực trị thì phương trình y ' = 0 có 3 nghiệm phân biệt. Và khi hàm số trên có ba cực trị thì ba cực trị đó luôn tạo thành một tam giác cân.
Cách giải: Ta có: y ' = 4 x 3 − 4 m x = 0 ⇔ x = 0 x 2 = m
Để phương trình y ' = 0 có 3 nghiệm phân biệt ⇔ m > 0
⇒ y ' = 0 ⇔ x = 0 ⇒ y = 2 m 2 − m ⇒ A 0 ; 2 m 2 − m x = m ⇒ y = m 2 − m ⇒ B m ; m 2 − m x = − m ⇒ y = m 2 − m ⇒ C − m ; m 2 − m
Ta có tam giác ABC luôn là tam giác cân tại A nên để ABC là tam giác vuông cân thì ta cần thêm điều kiện tam giác ABC vuông tại A ⇒ A B → . A C → = 0
A B → = m ; − m 2 ; A C → = − m ; − m 2
⇒ − m + m 4 = 0 ⇔ m m 3 − 1 = 0 ⇔ m = 0 k t m m = 1 t m
Vậy m=1

Đáp án là B
Cách 1. Sử dụng công thức tính nhanh ta có
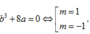
Cách 2. Nhận xét m thỏa mãn thì –m cũng thỏa mãn và hàm số có 3 điểm cực trị khi và chỉ khi m≠ 0 suy ra chọn B

Đáp án D
TXĐ: D = ℝ .
y ' = 4 x 3 + 2 6 m − 4 x = 0 ⇔ 4 x x 2 + 3 m − 2 = 0 ⇔ x = 0 x = ± 2 − 3 m .
Để đồ thị hàm số có ba điểm cực trị thì m < 2 3
Đồ thị hàm số có các điểm cực trị là M 0 ; 1 − m , A − 2 − 3 m ; − 9 m 2 + 11 m − 3 , B 2 − 3 m ; − 9 m 2 + 11 m − 3 .
Để tam giác MAB vuông tại M thì M A → . M B → = 0 hay
− 2 − 3 m + − 9 m 2 + 11 m − 3 − 1 + m 2 = 0 ⇔ − 9 m 2 + 12 m − 4 2 − 2 − 3 m = 0 ⇔ 2 − 3 m 4 − 2 − 3 m = 0 ⇔ 2 − 3 m = 0 l o a i 2 − 3 m = 1 ⇔ m = 1 3 .
Vậy m = 1 3 thỏa mãn điều kiện đề bài.

Đáp án là B
TXĐ D= ℝ
Cách 1.
Ta có: y ' = 4 x 3 − 4 m x = 4 x x 2 − m
Do hàm số đã cho là hàm số trùng phương nên để đồ thị hàm số y = x 4 − 2 m x 2 + 2 m − 3 có ba điểm cực trị là ba đỉnh của một tam giác cân thì phương trình y ¢= 0 phải có 3 nghiệm thực phân biệt.
Û x 2 = m có hai nghiệm phân biệt x ¹ 0 Û m > 0 .
Cách 2. (Dùng cho trắc nghiệm)
Do hàm số đã cho là hàm số trùng phương nên để đồ thị hàm số y = x 4 − 2 m x 2 + 2 m − 3 có ba điểm cực trị là ba đỉnh của một tam giác cân thì a . b < 0 ⇔ 1. − 2 m < 0 ⇔ m > 0.


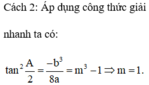


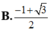
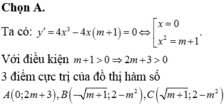


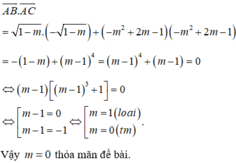
Đáp án là C