Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Số tam giác tạo được là;
\(C^2_{12}\cdot3+C^3_{12}=418\)
b: Số tam giác tạo thành là:
\(C^2_9\cdot6+C^3_9=300\)

AB đi qua E và vuông góc BC nên nhận (1;-1) là 1 vtpt
Phương trình AB:
\(1\left(x+1\right)-1\left(y-1\right)=0\Leftrightarrow x-y+2=0\)
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x-y+2=0\\x+y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(-3;-1\right)\)
Đường thẳng d qua M và song song AB có pt:
\(1\left(x+1\right)-1\left(y+1\right)=0\Leftrightarrow x-y=0\)
Gọi N là giao điểm d và BC \(\Rightarrow N\) là trung điểm BC
Tọa độ N là nghiệm: \(\left\{{}\begin{matrix}x-y=0\\x+y-4=0\end{matrix}\right.\) \(\Rightarrow N\left(2;2\right)\Rightarrow C\left(7;5\right)\)
Đường thẳng AD qua M và song song BC có pt:
\(1\left(x+1\right)+1\left(y+1\right)=0\Leftrightarrow x+y+2=0\)
A là giao điểm AB và AD nên tọa độ là nghiệm: \(\left\{{}\begin{matrix}x-y+2=0\\x+y+2=0\end{matrix}\right.\) \(\Rightarrow A\left(-2;0\right)\)
\(\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow\) tọa độ D

Tính số đường thẳng: Gọi X là tập hợp các điểm đã cho, S là tập hợp các điểm thẳng hàng và \(T=X\backslash S\). Qua 5 điểm thuộc S, ta vẽ được duy nhất 1 đường thẳng. Xét 1 điểm bất kì trong S, nó kết nối với 15 điểm không thuộc S bằng 1 đường thẳng. Tương tự với các điểm còn lại trong S, số đường thẳng nối từ các điểm thuộc S đến các điểm còn lại là \(5.15=75\) đường. Xét các điểm thuộc T, do trong các điểm thuộc T không có 3 điểm nào thẳng hàng nên số đường thẳng kết nối 15 điểm này là \(C^2_{15}\). Vậy có tất cả \(1+75+C^2_{15}=181\) đường thẳng từ 20 điểm đã cho.
Tính số tam giác: Xét 2 điểm bất kì thuộc S, có 15 tam giác được tạo thành từ 2 điểm đó và 1 điểm thuộc T. Số cách chọn 2 điểm thuộc S là \(C^2_5\), do đó số tam giác tạo thành bằng cách chọn 2 điểm thuộc S và 1 điểm thuộc T là \(C^2_5.15\). Xét 3 điểm bất kì thuộc T, có tất cả \(C^3_{15}\) tam giác. Vậy có tất cả \(C^2_5.15+C^3_{15}=605\) tam giác được tạo thành từ 20 điểm đã cho.

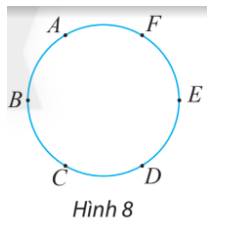
a) Một đoạn thẳng được tạo bởi 2 điểm bất kì
Nên để có một đoạn thẳng có điểm mút thuộc các điểm đã cho thì ta chọn 2 điểm bất kì từ 6 điểm đã cho, mỗi cách chọn 2 điểm từ 6 điểm đã cho là một tổ hợp chập 2 của 6, từ đó số đoạn thẳng có điểm đầu mút thuộc các điểm đã cho được tạo ra là:
\(C_6^2 = \frac{{6!}}{{2!.4!}} = 15\) (đoạn thẳng)
b) Mỗi tam giác được tạo bởi 3 điểm không thẳng hàng, nên để có một tam giác mà các đỉnh của nó là các điểm đã cho thì ta chọn 3 điểm bất kì từ 6 điểm đã cho, mỗi cách chọn 3 điểm từ 6 điểm là một tổ hợp chập 3 của 6, từ đó số tam giác có đỉnh thuộc các điểm đã cho là:
\(C_6^3 = \frac{{6!}}{{3!.3!}} = 20\) (tam giác)

A B C A' B' C' D E
Qua A vẽ đường thẳng vuông góc với CA', cắt CC' tại D.
Nối BA'. Qua A vẽ đường thẳng vuông góc với BA', cắt BB' tại E.
mp (AED) là mặt phẳng P cần tìm.
Bạn tự chứng minh nhé.
ok thanks bạn nhé. mình cũng vẽ kiểu này nhưng không biết chứng minh. giờ chứng minh đc r. :d

Ta có : HA.HB=OH²=1 (không đổi).
và AB=HA+HB ≥ 2√(HA.HB) = 2.√OH² = 2.
-> AB ≥ 2.
Vậy AB có độ dài nhỏ nhất là 2 khi HA=HB
Khi đó tg OHB và OHA vuông cân và có cạnh góc vuông = 1.
suy ra OA = OB =√2.
Vậy đoạn AB nhỏ nhất khi A(√2;0) B(0;√2).