Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mỗi cách cắm 4 bông hoa vào 4 bình hoa khác nhau (mỗi bông hoa cắm vào một bình) là một hoán vị của 4 phần tử.
Số cách cắm hoa là: 4!= 24
Chọn B.

+) Số cách chọn 5 bông hoa bất kì trong 110 bông hoa là: \(C_{110}^5\) ( cách chọn)
+) Số cách chọn 5 bông cúc trong 60 bông cúc là: \(C_{60}^5\) ( cách chọn)
+) Số cách chọn 5 bông hoa hồng trong 50 bông hồng là: \(C_{50}^5\) ( cách chọn)
+) Số cách chọn 5 bông hoa gồm cả 2 loại trong 110 bông hoa là: \(C_{110}^5 - C_{60}^5 - C_{50}^5\) ( cách chọn)

Số phần tử của không gian mẫu: `n(Ω) = C_12^4=495`
A: "4 bông được chọn có đủ 2 loại"``
`=> overline(A)`: "4 bông được chọn không đủ 2 loại"
``
TH1: không có hoa hồng
`=> C_7^0 . C_5^4=5`
TH2: không có đồng tiền
`=> C_7^4 . C_5^0 = 35`
`=>n(overline(A))=5+35=40`
``
`=> P(A)=1-P(overline(A))=1-40/495=91/99`

+) Mỗi lần lấy ngẫu nhiên ra 4 bông hoa từ 30 bông hoa ta có một tổ hợp chập 4 của 30. Do đó số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{30}^4\) (phần tử)
+) Gọi A là biến cố “ bốn bông hoa chọn ra có cả ba màu”
+) Để chọn ra bốn bông hoa có đủ 3 màu ta chia ra làm ba trường hợp:
TH1: 2 bông trắng, 1 bông vàng, 1 bông đỏ: \(C_{10}^2.10.10\) (cách chọn)
TH2: 1 bông trắng, 2 bông vàng, 1 bông đỏ: \(10.C_{10}^2.10\) (cách chọn)
TH3: 1 bông trắng, 1 bông vàng, 2 bông đỏ: \(10.10.C_{10}^2\) (cách chọn)
+) Áp dụng quy tắc cộng, ta có \(n\left( A \right) = 13500\) ( cách chọn)
+) Xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{100}}{{203}}\)

Mỗi lần lấy ngẫu nhiên ra 10 bông hoa từ 30 bông hoa ta có một tổ hợp chập 10 của 30. Do đó số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{30}^{10}\) (phần tử)
Gọi A là biến cố “Trong 10 bông hoa được chọn ra có ít nhất một bông màu trắng”
Vậy \(\overline A \) là biến cố “Trong 10 bông hoa được chọn ra đều là hoa màu vàng”
Mỗi cách lấy ra đồng thời 10 bông hoa từ 15 bông hoa màu vàng là một tổ hợp chập 10 của 15 phần tử. Vậy số phần tử của biến cố \(\overline A \) là : \(n\left( {\overline A } \right) = C_{15}^{10}\) ( phần tử)
Xác suất của biến cố \(\overline A \) là: \(P\left( {\overline A } \right) = \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega \right)}} = \frac{1}{{10005}}\)
Xác suất của biến cố A là: \(P\left( A \right) = 1 - P\left( {\overline A } \right) = \frac{{10004}}{{10005}}\)

Chọn A.
Gọi x là số điểm trong lần kiểm tra cuối mà Hoa cần đạt được để được cấp chứng chỉ.
Ta có số điểm qua 5 lần thi của Hoa là 64,5.5 = 322,5 suy ra:
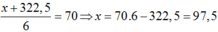

Dễ thấy: Hoa hồng nhung là loại hoa bán được nhiều nhất trong dịp năm nay, do đó cửa hàng nên nhập loại hoa này nhiều nhất để bán vào dịp 14 tháng 2 năm sau.

a) Số cách viết một dãy 5 chữ cái in hoa từ bảng chữ cái tiếng Anh (gồm 26 chữ cái) là: \({26^5}\)
b) Số cách viết một dãy 5 chữ cái in hoa khác nhau từ bảng chữ cái tiếng Anh (gồm 26 chữ cái) là: \(A_{26}^5\)
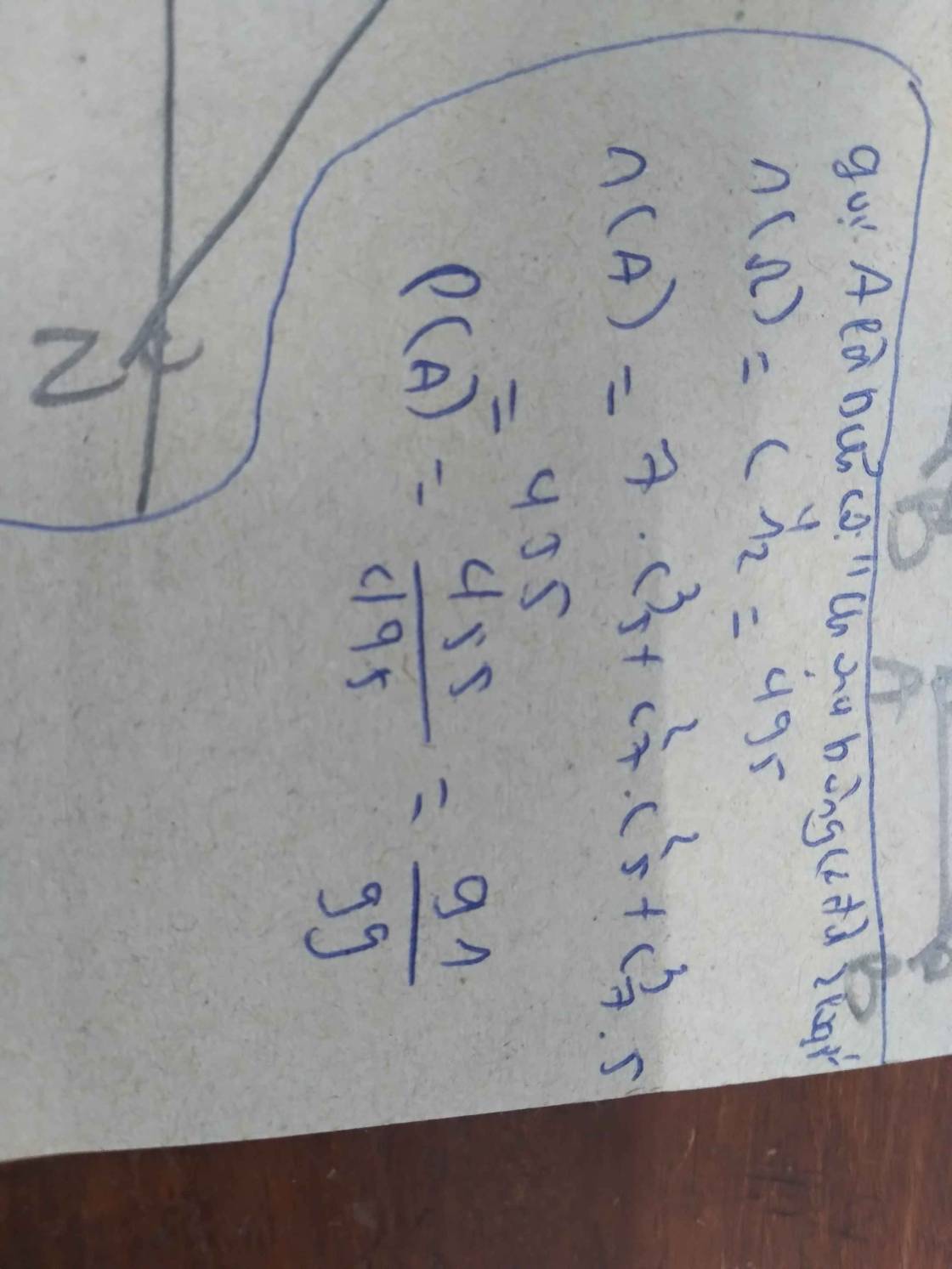
Dạ ai có thể giúp mình giải bài này với ạ
Số cách cắm 5 bông hoa vào 5 bình hoa là: 5! = 5.4.3.2.1 = 120 cách