K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
giúp mk bài này vs mk ko bt trình bày bài giải s cả
mong m.n giúp mk
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 11 2021
Do \(2\in[2;+\infty)\Rightarrow\) khi \(x=2\) thì \(f\left(x\right)=\dfrac{2\sqrt{x+2}-3}{x-1}\Rightarrow f\left(2\right)=\dfrac{2\sqrt{2+2}-3}{2-1}=1\)
\(-2\in\left(-\infty;2\right)\) \(\Rightarrow\) khi \(x=-2\) thì \(f\left(x\right)=x^2-1\Rightarrow f\left(-2\right)=\left(-2\right)^2-1=3\)
\(\Rightarrow P=1+3=4\)
29 tháng 10 2021
Vì khi đó hai vecto AB,AC sẽ cùng phương
=>AB//AC
mà AB và AC có điểm chung là A
nên A,B,C thẳng hàng
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 11 2021
a.
Phương trình có 2 nghiệm trái dấu khi và chỉ khi:
\(ac< 0\Leftrightarrow1.\left(2m+1\right)< 0\)
\(\Leftrightarrow m< -\dfrac{1}{2}\)
b.
Phương trình có 2 nghiệm nằm cùng phía trục Oy \(\Leftrightarrow\) phương trình có 2 nghiệm cùng dấu
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=\left(m+1\right)^2-\left(2m+1\right)>0\\x_1x_2=2m+1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m>-\dfrac{1}{2}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
a.
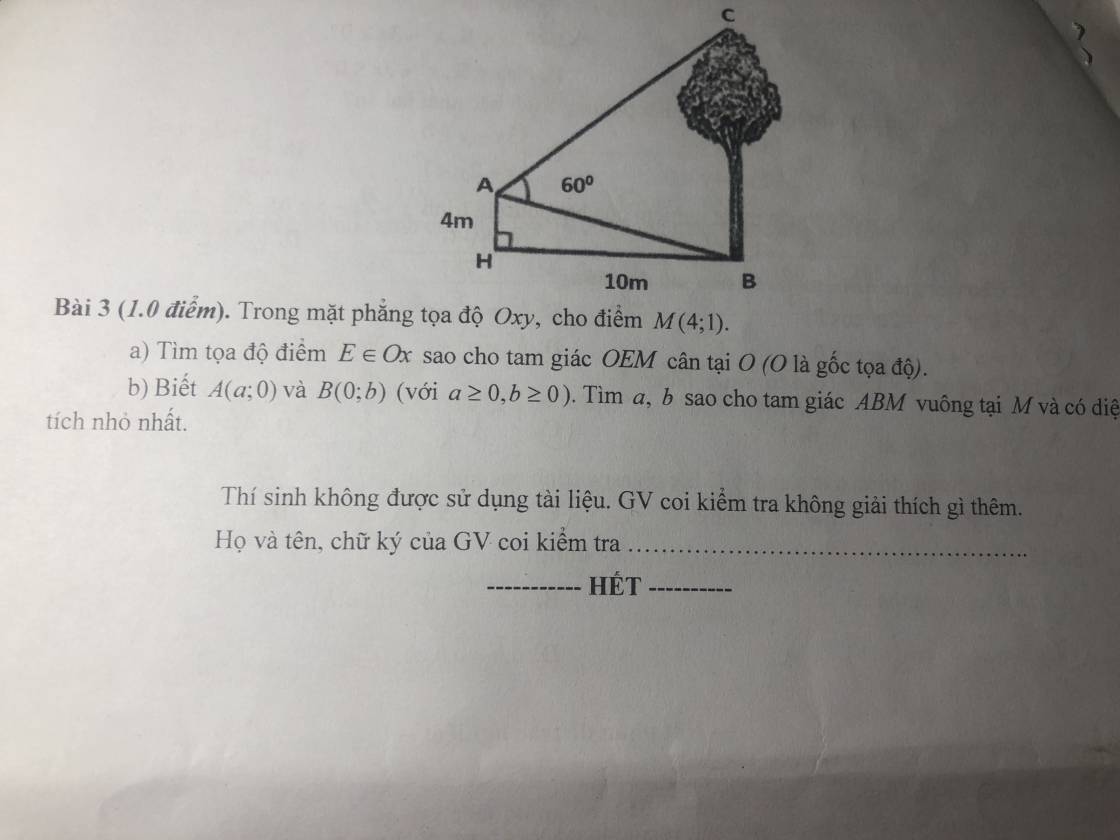
D E thuộc Ox \(\Rightarrow\) tọa độ E có dạng \(E\left(x;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{OE}=\left(x;0\right)\\\overrightarrow{OM}=\left(4;1\right)\end{matrix}\right.\)
Tam giác OEM cân tại O \(\Rightarrow OE=OM\)
\(\Rightarrow\sqrt{x^2+0^2}=\sqrt{4^2+1^2}\Rightarrow x^2=17\)
\(\Rightarrow x=\pm\sqrt{17}\Rightarrow\left[{}\begin{matrix}E\left(\sqrt{17};0\right)\\E\left(-\sqrt{17};0\right)\end{matrix}\right.\)
b.
\(\left\{{}\begin{matrix}\overrightarrow{MA}=\left(a-4;-1\right)\\\overrightarrow{MB}=\left(-4;b-1\right)\end{matrix}\right.\)
Tam giác ABM vuông tại M \(\Rightarrow\overrightarrow{MA}.\overrightarrow{MB}=0\)
\(\Rightarrow-4\left(a-4\right)-1\left(b-1\right)=0\)
\(\Leftrightarrow4a+b-17=0\Rightarrow b=17-4a\)
Lại có \(S_{ABM}=\dfrac{1}{2}MA.MB=\dfrac{1}{2}\sqrt{\left(a-4\right)^2+1}.\sqrt{\left(b-1\right)^2+16}\)
\(=\dfrac{1}{2}\sqrt{\left(a-4\right)^2+1}.\sqrt{\left(16-4a\right)^2+16}=\dfrac{1}{2}\sqrt{\left(a-4\right)^2+1}.\sqrt{16\left[\left(a-4\right)^2+1\right]}\)
\(=2\left[\left(a-4\right)^2+1\right]\ge2\)
Dấu "=" xảy ra khi \(a-4=0\Rightarrow a=4\Rightarrow b=1\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
2.
Gọi \(H\left(x;y\right)\) là toạ độ chân đường cao ứng với BC \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}=\left(x-1;y+2\right)\\\overrightarrow{BC}=\left(2;1\right)\end{matrix}\right.\)
Do AH vuông góc BC \(\Rightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)
\(\Rightarrow2\left(x-1\right)+y+2=0\Leftrightarrow y=-2x\)
\(\Rightarrow H\left(x;-2x\right)\Rightarrow\overrightarrow{BH}=\left(x+2;-2x-3\right)\)
Do H thuộc BC nên B, C, H thẳng hàng hay các vecto \(\overrightarrow{BC};\overrightarrow{BH}\) cùng phương
\(\Rightarrow\dfrac{x+2}{2}=\dfrac{-2x-3}{1}\Rightarrow x=\dfrac{8}{5}\Rightarrow y=-\dfrac{16}{5}\) \(\Rightarrow H\left(-\dfrac{8}{5};\dfrac{16}{5}\right)\)
\(\Rightarrow\overrightarrow{AH}=\left(-\dfrac{13}{5};\dfrac{26}{5}\right)\Rightarrow\left\{{}\begin{matrix}AH=\sqrt{\left(-\dfrac{13}{5}\right)^2+\left(-\dfrac{6}{5}\right)^2}=\dfrac{13\sqrt{5}}{5}\\BC=\sqrt{2^2+1^2}=\sqrt{5}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{13}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
3.
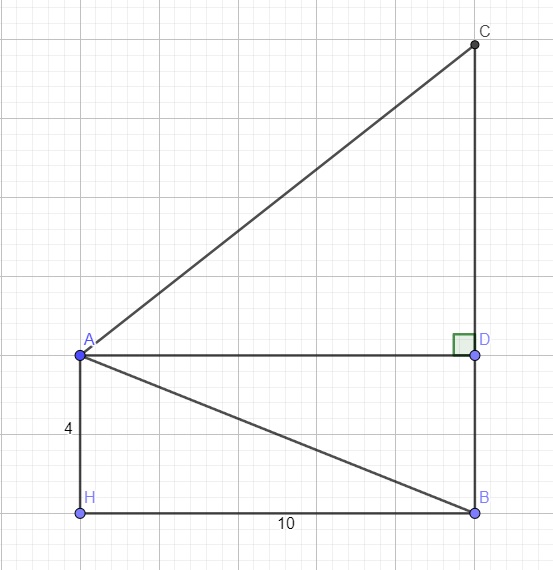
Kẻ AD vuông góc BC tại D
\(\Rightarrow AD=BH=10\) ; \(BD=AH=4\)
\(tan\widehat{BAD}=\dfrac{BD}{AD}=\dfrac{2}{5}\Rightarrow\widehat{BAD}\approx21^048'5''\)
\(\Rightarrow\widehat{CAD}=60^0-\widehat{BAD}=38^011'55''\)
\(\Rightarrow CD=AD.tan\widehat{CAD}=7,87\left(m\right)\)
\(\Rightarrow BC=BD+CD=11,87\left(m\right)\)
5 tháng 11 2021
Bài 6:
b: PTHĐGĐ là:
\(x^2+4x-1=x-3\)
\(\Leftrightarrow x^2+3x-4=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=-7\\y=-2\end{matrix}\right.\)
PK
5
TA
18 tháng 5 2021
`sin3x sinx+sin(x-π/3) cos (x-π/6)=0`
`<=> 1/2 (cos2x - cos4x) + 1/2(-sin π/6 + sin (2x-π/2)=0`
`<=> cos2x-cos4x-1/2+ sin(2x-π/2)=0`
`<=>cos2x-cos4x-1/2+ sin2x .cos π/2 - cos2x. sinπ/2=0`
`<=> cos2x - cos4x - cos2x = 1/2`
`<=> cos4x = cos(2π)/3`
`<=>` \(\left[{}\begin{matrix}4x=\dfrac{2\text{π}}{3}+k2\text{π}\\4x=\dfrac{-2\text{π}}{3}+k2\text{π}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\\x=-\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\end{matrix}\right.\)
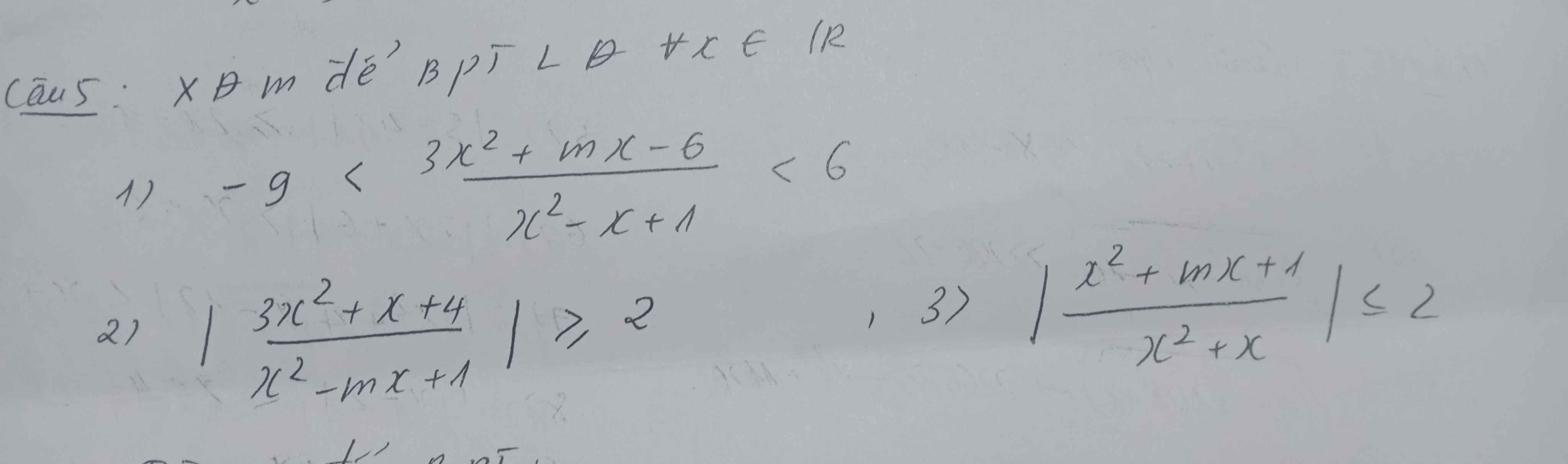
có ghi ra tiếng việt thì tui làm chớ tiếng anh thì chệu
ko lm đc thì thôi