Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta thấy hai biến cố :”Hai quả bóng lây ra cùng màu” và “Hai quả bóng lấy ra khác màu” là hai biến cố đối
Suy ra xác suất của biến cố “Hai quả bóng lây ra cùng màu” là \(1 - 0,6 = 0,4\)

Chia 16 số ra làm 3 tập:
A={1;4;7;10;13;16}; B={2;5;8;11;14}; C={3;6;9;12;15}
TH1: 1 số trong A, 1 số trong B, 1 số trong C
=>Có 6*5*5=150 cách
TH2: 3 số trong A
=>Có \(C^3_6=20\left(cách\right)\)
TH3: 3 số trong B hoặc C
=>Có \(C^3_5\cdot2=20\left(cách\right)\)
=>n(A)=20+20+150=190
\(n\left(omega\right)=C^3_{16}=560\)
=>P(A)=19/56

Tổng số khả năng có thể xảy ra của phép thử là \(n\left( \Omega \right) = C_{13}^2.13\)
a) Biến cố “Ba quả bóng lấy ra cùng màu” xảy ra khi hai lần đều lấy ra bóng có cùng màu xanh, đỏ hoặc vàng. Số kết quả thuận lợi cho biến cố là \(C_5^2.5 + C_6^2.6 + C_2^2.2 = 142\)
Vậy xác suất của biến cố “Ba quả bóng lấy ra cùng màu” là \(P = \frac{{142}}{{13C_{13}^2}} = \frac{{71}}{{507}}\)
b) Số kết quả thuận lợi cho biến cố “Bóng lấy ra lần 2 là bóng xanh” là \(C_{13}^2.5\)
Vậy xác suất của biến cố “Bóng lấy ra lần 2 là bóng xanh” là \(P = \frac{{5C_{13}^2}}{{13C_{13}^2}} = \frac{5}{{13}}\)
c) Biến cố “Ba bóng lấy ra có ba màu khác nhau” xảy ra khi hai quả bóng lấy ra lần đầu là 2 màu khác nhau và quả bóng lấy lần 2 có màu còn lại. Số kết quả thuận lợi cho biến cố này là \(5.6.2.3 = 180\)
Vậy xác suất của biến cố “Ba bóng lấy ra có ba màu khác nhau” là \(P = \frac{{180}}{{13C_{13}^2}} = \frac{{30}}{{169}}\)
Cái này nhân 3 TH thui
VD (xanh+đỏ; vàng) ; (xanh+vàng; đỏ); (đỏ+vàng;xanh) nên x3 chứ không phải nhân 3! á em (câu c)

Do lần đầu tiên lấy bóng sau đó trả lại hộp nên lần hai có thể lấy 1 trong 4 quả bóng và hai lần lấy lần lượt nên ta cần phải tính đến thứ tự lấy bóng. Nếu lần đầu lấy được bóng 1 và lần hai lấy được bóng 3 thì ta sẽ kí hiệu kết quả của phép thử là cặp (1; 3). Khi đó không gian mẫu của phép thử là:
\(\Omega = \left\{ \begin{array}{l}(1;1);(1;2);(1;3);(1;4);(2;1);(2;2);(2;3);(2;4);\\(3;1);(3;2);(3;3);(3;4);(4;1);(4;2);(4;3);(4;4)\end{array} \right\}\)

Số phần tử của không gian mẫu \(\left|\Omega\right|=C^2_{20}\)
Gọi A là biến cố: "Tổng hai số trên hai tấm thẻ được rút ra bằng 10."
Gọi \(\left(m,n\right)\) là nghiệm của \(m+n=10\). Phương trình này có tất cả \(C^{2-1}_{10-1}-1=8\) (\(-1\) ở đây là bỏ đi nghiệm \(\left(m;n\right)=\left(5;5\right)\)). Do đó \(\left|A\right|=8\) \(\Rightarrow P\left(A\right)=\dfrac{\left|A\right|}{\left|\Omega\right|}=\dfrac{8}{C^2_{20}}=\dfrac{4}{95}\)

+) Số trung bình: \(\overline x = \frac{{0.10 + 1.30 + 2.40 + 3.20}}{{100}} = 1,7\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm, \(\underbrace {0,...,0}_{10},\underbrace {1,...,1}_{30},\underbrace {2,...,2}_{40},\underbrace {3,...,3}_{20}.\)
Bước 2: Vì \(n = 100\), là số chẵn nên \({Q_2} = \frac{1}{2}(2 + 2) = 2\)
\({Q_1}\) là trung vị của nửa số liệu: \(\underbrace {0,...,0}_{10},\underbrace {1,...,1}_{30},\underbrace {2,...,2}_{10}.\) Do đó \({Q_1} = \frac{1}{2}(1 + 1) = 1\)
\({Q_3}\) là trung vị của nửa số liệu \(\underbrace {2,...,2}_{30},\underbrace {3,...,3}_{20}.\) Do đó \({Q_3} = \frac{1}{2}(2 + 2) = 2\)
+) Mốt \({M_o} = 2\)

Để quả bóng có thể ném được qua lưới cao 2 m thì \(y = f\left( x \right) = - 0,03{x^2} + 0,4x + 1,5 > 2\)
\( \Rightarrow f\left( x \right) = - 0,03{x^2} + 0,4x - 0,5 > 0\)
Xét tam thức \(f\left( x \right) = - 0,03{x^2} + 0,4x - 0,5\) có \(\Delta = 0,1 > 0\), có hai nghiệm phân biệt là \({x_1} \simeq 1,4;{x_2} \simeq 11,9\) và có \(a = - 0,03 < 0\)
Ta có bảng xét dấu như sau
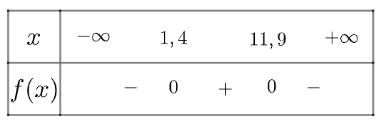
Vậy để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới từ 1,4 cho đến 11,9 mét

a) Việc xếp 9 viên bi sao cho không có hai viên bi trắng nào xếp liến nhau được thực hiện qua 2 công đoạn
Công đoạn 1: Xếp 4 viên bi xanh trước, vì các viên bi có kích thước khác nhau nên quan tâm đến thứ tự, suy ra công đoạn 1 có \(4! = 24\) cách
Công đoạn 2: Xếp 5 viên bi trắng vào 5 vị trí xung quanh bi xanh, có quan tâm đến thứ tự nên công đoạn 2 có \(5! = 120\) cách
Vậy có \(120.24 = 2880\) kết quả thuận lợi cho biến cố “Không có hai viên bi trắng nào xếp liền nhau”
b) Việc xếp 9 viên bi sao cho bốn viên bi xanh được xếp liền nhau được thực hiện qua 2 công đoạn
Công đoạn 1: Xếp 4 viên bi xanh liền nhau, vì các viên bi có kích thước khác nhau nên quan tâm đến thứ tự, suy ra công đoạn 1 có \(4! = 24\) cách
Công đoạn 2: Xếp 5 viên bi trắng có kích thước khác nhau vào bên trái hay bên phải của bi xanh, có quan tâm đến thứ tự nên công đoạn 2 có \(5!{.2^5} = 3840\) cách
Vậy có \(3840.24 = 92160\) kết quả thuận lợi cho biến cố “Bốn viên bi xanh được xếp liền nhau”

Có đúng 1 bộ số là (1,2,3,4) có tổng bằng 10
Không gian mẫu: \(A_6^4\)
Chọn bộ số 1,2,3,4 có 1 cách, xếp chúng theo hàng ngang có \(4!\) cách
Xác suất: \(P=\dfrac{4!}{A_6^4}=\dfrac{1}{15}\)