Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: SỐ cách chọn là 4+3=7 cách
b: Số cách chọn là 4*3=12 cách

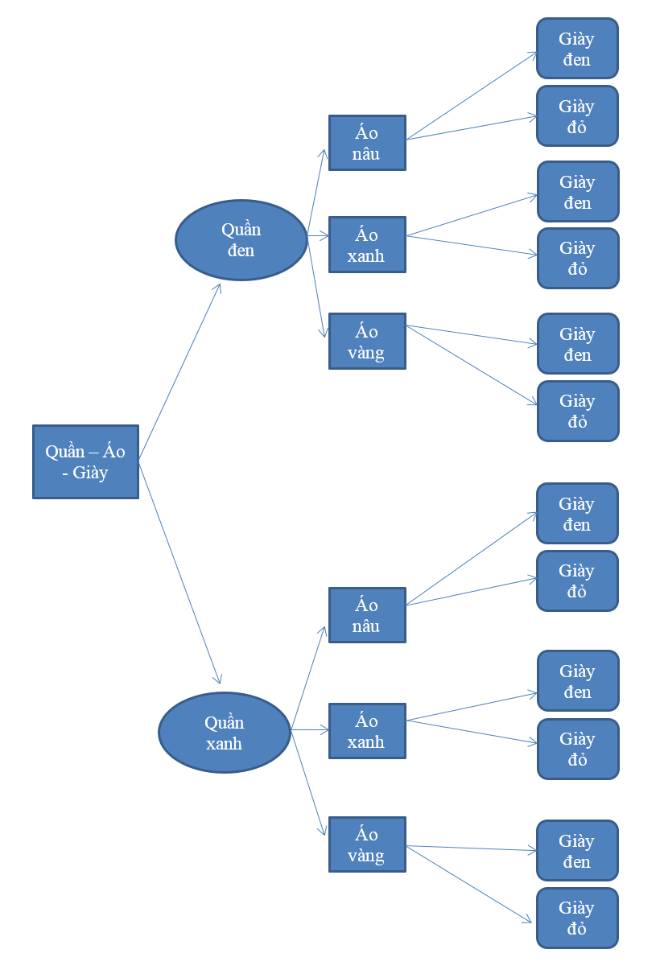
Kết luận: Từ sơ đồ cây, ta thấy bạn Dương có 12 cách chọn một bộ quần áo và một đôi giày.

Như hpt lớp 8.
Gọi giá bán áo là x , giá bán quần là y, giá bán váy là z.
Theo đề bài ta có :
\(\left\{{}\begin{matrix}12x+21y+18z=5349000\\16x+24y+12z=5600000\\24x+15y+12z=5259000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=98000\\y=125000\\z=86000\end{matrix}\right.\)
Vậy giá bán áo là 98000 đồng, giá bán quần là 125000 đồng, giá bán váy là 86000 đồng.
Gọi giá tiền mỗi cái áo là \(x\) (đồng), giá tiền mỗi cái quần là \(y\) (đồng), giá tiền mỗi cái váy là \(z\) (đồng)
ĐK : \(x,y,z\in N^{\circledast}\)
Vì ngày thứ nhất bán được 12 áo, 21 quần và 18 váy, doanh thu 5 349 000 đồng nên
ta có phương trình : \(12x+21y+18z=5349000\) (1)
Vì ngày thứ hai bán được 16 áo, 24 quần và 12 váy, doanh thu 5 600 000 đồng nên
ta có phương trình : \(16x+24y+12z=5600000\) (2)
Vì ngày thứ ba bán được 24 áo, 15 quần và 12 váy, doanh thu 5 259 000 đồng nên
ta có phương trình : \(24x+15y+12z=5259000\) (3)
Từ (1),(2) và (3) ta có hệ phương trình :
\(\left\{{}\begin{matrix}12x+21y+18z=5349000\\16x+24y+12z=5600000\\24x+15y+12z=5259000\end{matrix}\right.\)
Giải hệ phương trình : \(\left\{{}\begin{matrix}12x+21y+18z=5349000\\16x+24y+12z=5600000\\24x+15y+12z=5259000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=98000\left(TM\right)\\y=125000\left(TM\right)\\z=86000\left(TM\right)\end{matrix}\right.\)
Vậy giá tiền mỗi cái áo là 98000 đồng, giá tiền mỗi cái quần là 125000, giá tiền mỗi cái váy là 86000 đồng

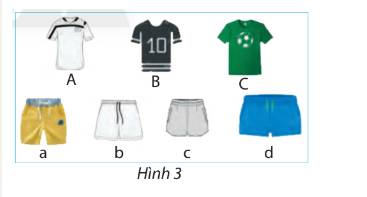
a)
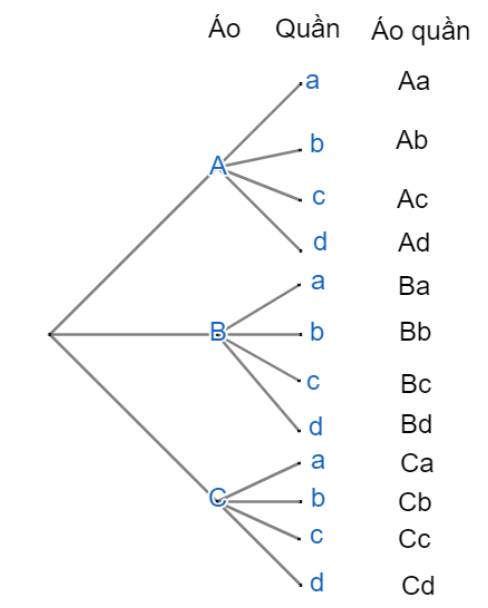
b) An có 12 cách chọn một bộ quần áo
vì: Để chọn một bộ quần áo bao gồm chọn quần riêng và áo riêng
Có 3 cách chọn một chiếc áo
Vì 4 cái quần khác nhau nên với mỗi cái áo riêng thì sẽ có 4 cách chọn 1 cái quần để tạo thành một bộ quần áo
Tương tự như vậy với hai cái áo còn lại, nên tổng cộng sẽ có 12 cách chọn một bộ quần áo (hay nhìn vào sơ đồ ta thấy rằng có 12 bộ quần áo)

Gọi x, y, z (đồng) lần lượt là giá tiền mỗi áo, quần và váy (0 < x, y, z < 5259000).
Ngày thứ nhất bán được 21 áo, 21 quần và 18 váy, doanh thu là 5.349.000 đồng nên ta có:
12x + 21y + 18z = 5.349.000
Ngày thứ hai bán được 16 áo, 24 quần và 12 váy, doanh thu là 5.600.000 đồng nên ta có:
16x + 24y + 12z = 5.600.000
Ngày thứ ba bán được 24 áo, 15 quần và 12 váy, doanh thu là 5.259.000 đồng nên ta có:
24x + 15y + 12z = 5.259.000
Từ đó ta có hệ phương trình:
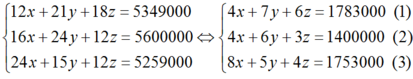
Lấy (1) – (2) ta được : y + 3z = 383000.
Nhân 2 vào hai vế của (1) rồi trừ đi (3) ta được: 9y + 8z = 1813000
Ta có hệ phương trình:
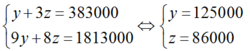
Thay y = 125000, z = 86000 vào (1) ta được x = 98000.
Vậy: Giá bán mỗi áo là: 98.000 đồng.
Giá bán mỗi quần là: 125.000 đồng.
Giá bán mỗi váy là: 86.000 đồng.

a) Chú ý rằng với hai người \(A\)và \(B\)thi đấu với nhau thì \(A\)thi đấu với \(B\)và \(B\)thi đấu với \(A\).
Mỗi người sẽ đấu với \(n-1\)người, nên tổng số ván đấu của giải là:
\(\frac{n\left(n-1\right)}{2}\).
b) Giả sử \(n=12\).
Tổng số ván đấu của giải là: \(\frac{12.11}{2}=66\).
Tổng số điểm của tất cả các kì thủ là: \(2\times66=132\).
Kì thủ cuối thắng ba kì thủ đứng đầu, do đó số điểm kì thủ cuối ít nhất là \(2.3=6\).
Do số điểm các kì thủ đôi một khác nhau nên tổng số điểm tối thiểu của tất cả các kì thủ là:
\(6+7+8+9+10+11+12+13+14+15+16+17=138>132\).
Do đó không thể xảy ra điều này.
Ta có đpcm.

a) Đội A:
+) Số trung bình: \(\overline x = \frac{{28 + 24 + 26 + 25 + 25 + 23 + 20 + 29 + 21 + 24 + 24}}{{11}} = 24,45\)
+) Mốt: \({M_o} = 24\)
+) Phương sai \({S^2} = \frac{1}{{11}}\left( {{{28}^2} + {{24}^2} + ... + {{24}^2}} \right) - 24,{45^2} = 6,65\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 2,58\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 20, 21, 23, 24, 24, 24, 25, 25, 26, 28, 29
\({Q_2} = {M_e} = 24\)
\({Q_1}\) là trung vị của nửa số liệu: 20, 21, 23, 24, 24. Do đó \({Q_1} = 23\)
\({Q_3}\) là trung vị của nửa số liệu: 25, 25, 26, 28, 29. Do đó \({Q_3} = 26\)
Đội B:
+) Số trung bình: \(\overline x = \frac{{32 + 20 + 19 + 21 + 28 + 29 + 21 + 22 + 29 + 19 + 29}}{{11}} = 24,45\)
+) Mốt: \({M_o} = 29\)
+) Phương sai \({S^2} = \frac{1}{{11}}\left( {{{32}^2} + {{20}^2} + ... + {{29}^2}} \right) - 24,{45^2} = 22,12\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 4,7\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 19, 19, 20, 21, 21, 22, 28, 29, 29, 29, 32.
\({Q_2} = {M_e} = 22\)
\({Q_1}\) là trung vị của nửa số liệu: 19, 19, 20, 21, 21. Do đó \({Q_1} = 20\)
\({Q_3}\) là trung vị của nửa số liệu: 28, 29, 29, 29, 32. Do đó \({Q_3} = 29\)
b)
Ta so sánh độ lệch chuẩn \(2,58 < 4,7\) do dó đội A có độ tuổi đồng đều hơn.
Chú ý
Ta không so sánh số trung vị vì không có giá trị nào quá lớn hay quá nhỏ so với các giá trị còn lại.