Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xem hỗn hợp ban đầu được tạo thành từ: Fe, Cu và O2
Fe -------> Fe3+ + 3e
x.........................3x
Cu -------> Cu2+ + 2e
y..........................2y
O2 + 4e -----> 2O2-
z.........4z
S+6 + 2e -------> S+4
...........0,045..........0,0225
Gọi x, y, z là số mol Fe, Cu, O2. Ta có hệ gồm 3 pt:
56x + 64y + 32z = 2,44
3x + 2y = 4z + 0,045
0,5*400x + 160y = 6,6
=> x = 0,025, y = 0,01, z = 0,0125
=> %mCu = 0,01*64/2,44*100% = 26,23%

Đáp án A
2 Al + Fe 2 O 3 → t o Al 2 O 3 + 2 Fe
Vì chia hỗn hợp Y thành hai phần bằng nhau nên số mol mỗi chất trong hai phần đều bằng nhau.
Vì phần 1 tác dụng với dung dịch NaOH có xuất hiện khí nên Y có Al.
Do đó Y có Al, Fe, A12O3 và có thể có Fe2O3.


Đáp án A
Cho phần 1 tác dụng với 0,4 mol NaOH thấy thoát ra 0,04 mol H2.
Do vậy Al dư 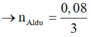
BTNT: ![]()
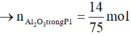
Ta có khối lượng mỗi phần là 39,44 gam.
![]()
Phần 2 tan trong HCl thu được dung dịch Z chứa 98,64 gam muối.
![]()
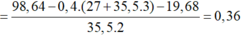
Giải được số mol Cr và Fe trong mỗi phần là 0,12 và 0,24 mol.
Bảo toàn O:
![]()
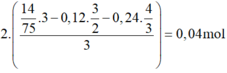

3.NO2 nhé
nNO2= 0,06 mol
PTHH:
Cu + 4HNO3→ Cu(NO3)2 + 2NO2+ 2H2O
x__________________________2x
Al+ 6HNO3→ Al(NO3)3+3NO2+3H2O
y______________________3y
Giải HPT:
\(\left\{{}\begin{matrix}64x+27y=1,23\\2x+3y=0,06\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=,015\\y=0,01\end{matrix}\right.\)
%Cu=\(\frac{0,015.64}{1,23}\text{.100%=78,048 %}\)
1.
Gọi số mol Mg và Al là a và b
nH2=0,4
Mg+2HCl\(\rightarrow\)MgCl2+H2
2Al+6HCl\(\rightarrow\)2AlCl3+3H2
Giải HPT:\(\left\{{}\begin{matrix}\text{ 24a+27b=7,8}\\\text{a+1,5b=0,4}\end{matrix}\right.\rightarrow\left\{{}\begin{matrix}a=0,1\\b=0,2\end{matrix}\right.\)
\(\rightarrow\)%mMg=\(\frac{0,1.24}{7,8}\)=30,77%
2.
Gọi số mol Zn, Al là a và b
3Zn+8HNO3\(\rightarrow\)3Zn(NO3)2+2NO+4H2O
Al+4HNO3\(\rightarrow\)Al(NO3)3+NO+2H2O
nNO=0,4
Giải HPT:
\(\left\{{}\begin{matrix}\text{65a+27b=11,9}\\\frac{2a}{3}\text{+b=0,4}\end{matrix}\right.\rightarrow\left\{{}\begin{matrix}a=\frac{11}{470}\\\frac{271}{705}\end{matrix}\right.\)
\(\rightarrow\)%mZn=\(\frac{65.\frac{11}{470}}{11,9}\)=12,78%


Gọi số mol Al, Fe2O3 mỗi phần lần lượt là a,b (mol) (a,b>0)
- Xét phần 2:
\(2Al+6HCl\rightarrow2AlCl_3+3H_2\\ n_{H_2\left(P2\right)}=\dfrac{4,48}{22,4}=0,2\left(mol\right)\\ n_{Al\left(P2\right)}=\dfrac{2}{3}.0,2=\dfrac{2}{15}\left(mol\right)\\ m_{Al\left(P2\right)}=\dfrac{2}{15}.27=1,8\left(g\right)\\ m_{P2}=\dfrac{40,1}{2}=20,05\left(g\right)\\ \%m_{\dfrac{Al\left(P2\right)}{P_2}}=\%m_{\dfrac{Al}{2Phần}}=\dfrac{1,8}{20,05}.100\approx8,978\%\)
P1: Do chất rắn tác dụng với NaOH có khí thoát ra
=> trong Y chứa Al
P2: Gọi (nAl; nFe; nAl2O3) = (a;b;c)
PTHH: 2Al + 6HCl --> 2AlCl3 + 3H2
a---------------------->1,5a
Fe + 2HCl --> FeCl2 + H2
b---------------------->b
=> 1,5a + b = \(\dfrac{4,48}{22,4}=0,2\left(mol\right)\) (1)
mY = mX = 40,1
=> 54a + 112b + 204c = 40,1 (2)
PTHH: 2Al + Fe2O3 --to--> Al2O3 + 2Fe
=> \(\dfrac{n_{Fe}}{n_{Al_2O_3}}=\dfrac{2}{1}\) => \(\dfrac{b}{c}=\dfrac{2}{1}\) (3)
(1)(2)(3) => \(\left\{{}\begin{matrix}a=\dfrac{9}{890}\left(mol\right)\\b=\dfrac{329}{1780}\left(mol\right)\\c=\dfrac{329}{3560}\left(mol\right)\end{matrix}\right.\)
=> nAl = 2.(a + 2c) = \(\dfrac{347}{890}\left(mol\right)\)
=> \(\%Al=\dfrac{27.\dfrac{347}{890}}{40,1}.100\%=26,252\%\)