Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

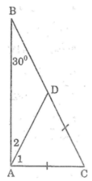
Xét ΔABC, ta có: ∠A= 90o; ∠B= 30o
Trên cạnh BC lấy điểm D sao cho CD = AC
Ta có: ΔACD cân tại C
Mà ∠C + ∠B = 90o (tính chất tam giác vuông)
Suy ra: ∠C = 90o - ∠B = 90o - 30o = 60o
Suy ra: ΔACD đều
Suy ra: AC = AD = DC và ∠A1= 60o
Ta có: ∠A1+ ∠A2 = ∠BAC = 90o
⇒ ∠A2 = 90o - ∠A1 = 90o - 60o = 30o
Trong ΔADB, ta có: ∠A2 = ∠B= 30o
Suy ra: ΔADB cân tại D (vì có 2 góc kề cạnh AB bằng nhau)
Hay AD = DB
Suy ra: AC = CD = DB mà CD + DB = BC
Vậy AC = 1/2 BC.

Với tam giác ABC có góc A=90 độ và góc B=30 độ
=> góc C=60 độ
Gọi M là trung điểm của BC
mà tam giác ABC có góc A bằng 90 độ
=>AM=BM=CM(định lý)
=>tam giác AMC cân tại M(dấu hiệu nhận biết)
mà góc C bằng 60 độ
=> tam giác AMC đều(dấu hiệu nhận biết)
=>AC=MC(đ/n)
mà MC =1/2.BC (gt)
=> AC = 1/2 BC (tcbc)
Ta có điều phải chứng minh
Với tam giác ABC có góc A=90 độ và góc B=30 độ
=> góc C=60 độ
Gọi M là trung điểm của BC
mà tam giác ABC có góc A bằng 90 độ
=>AM=BM=CM(định lý)
=>tam giác AMC cân tại M(dấu hiệu nhận biết)
mà góc C bằng 60 độ
=> tam giác AMC đều(dấu hiệu nhận biết)
=>AC=MC(đ/n)
mà MC =1/2.BC (gt)
=> AC = 1/2 BC (tcbc)
Ta có điều phải chứng minh
Xét \(\Delta\)ABC và \(\Delta\)A'B'C có :
\(\widehat{A}=\widehat{A'}=90^0\)
AC = A'C'
\(\widehat{B}=\widehat{B'}\)
Ta cần chứng minh \(\Delta\)ABC = \(\Delta\)A'B'C
Ta có : \(\widehat{C}=90^0-\widehat{B},\widehat{C'}=90^0-\widehat{B'}\)
mà \(\widehat{B}=\widehat{B'}\)nên \(\widehat{C}=\widehat{C'}\)
=> \(\Delta\)ABC = \(\Delta\)A'B'C(g.c.g)
Bạn tự vẽ hình nhé!
Tam giác bằng nhau theo TH: cạnh huyền,góc nhọn