K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 4 2021
\(A=2sin\dfrac{a+b}{2}cos\dfrac{a-b}{2}+2sin\dfrac{a+b}{2}cos\dfrac{a+b}{2}\)
\(=2sin\dfrac{a+b}{2}\left(cos\dfrac{a+b}{2}+cos\dfrac{a-b}{2}\right)\)
\(=2sin\dfrac{a+b}{2}.2cos\dfrac{a}{2}cos\dfrac{b}{2}\)
\(=4sin\dfrac{a+b}{2}cos\dfrac{a}{2}cos\dfrac{b}{2}\)
TN
0
TN
0
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 5 2020
\(0< A;B;C< 180^0\Rightarrow\left\{{}\begin{matrix}sinA>0\\sinB>0\\sinC>0\end{matrix}\right.\)
\(\Rightarrow A=sinA+sinB+sinC>0\)
\(B=sinA.sinB.sinC>0\)
Riêng 2 câu c;d đâu biết \(\alpha\) là góc nào mà xét dấu?
10 tháng 5 2021
Ta có: A = \(sin\dfrac{A}{2}+sin\dfrac{B}{2}+sin\dfrac{C}{2}=cos\dfrac{B+C}{2}+2sin\dfrac{B+C}{4}cos\dfrac{B-C}{4}\)
\(\Leftrightarrow A-2sin\dfrac{B+C}{4}cos\dfrac{B-C}{4}-cos^2\dfrac{B+C}{4}+sin^2\dfrac{B+C}{4}=0\)\(\Leftrightarrow A-2sin\dfrac{B+C}{4}cos\dfrac{B-C}{4}+2sin^2\dfrac{B+C}{4}-1=0\)
Δ' = \(cos^2\dfrac{B-C}{4}-2\left(A-1\right)\ge0\)
\(\Rightarrow A-1\le\dfrac{1}{2}\Leftrightarrow A\le\dfrac{3}{2}\)
AL
cho tam giác ABC, chứng minh rằng: \(sinA+sinB-sinC=4.sin\frac{A}{2}.sin\frac{B}{2}.cos\frac{C}{2}\)
1
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2019
\(sinA+sinB-sinC=2sin\frac{A+B}{2}cos\frac{A-B}{2}-sinC\)
\(=2cos\frac{C}{2}.cos\frac{A-B}{2}-2sin\frac{C}{2}cos\frac{C}{2}\)
\(=2cos\frac{C}{2}\left(cos\frac{A-B}{2}-sin\frac{C}{2}\right)\)
\(=2cos\frac{C}{2}\left(cos\frac{A-B}{2}-cos\frac{A+B}{2}\right)\)
\(=4cos\frac{C}{2}sin\frac{A}{2}sin\frac{B}{2}\)
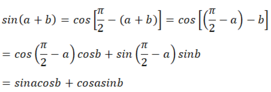
\(=2sin\left(\frac{a+b}{2}\right)cos\left(\frac{a-b}{2}\right)+2sin\left(\frac{a+b}{2}\right)cos\left(\frac{a+b}{2}\right)\)
\(=2sin\left(\frac{a+b}{2}\right)\left[cosa\left(\frac{a-b}{2}\right)+cos\left(\frac{a+b}{2}\right)\right]\)
\(=4sin\left(\frac{a+b}{2}\right)cos\frac{a}{2}.cos\frac{b}{2}\)