

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



B C A M D E
Giả sử cho tam giác ABC cân tại A, M là trung điểm của BC; từ M kẻ MD,ME lần lượt vuông góc với AB,AC tại D,E.
Bây giờ ta cần chứng minh MD=ME
Bài làm:
Vì M là trung điểm của BC
=> AM là trung tuyến của tam giác ABC; mà tam giác ABC cân tại A
=> AM đồng thời là đường phân giác của tam giác ABC
=> \(\widehat{BAM}=\widehat{MAC}\)(hoặc bạn có thể chứng minh \(\Delta AMB=\Delta AMC\left(c.c.c\right)\))
\(\Delta AMD=\Delta AME\left(c.h-g.n\right)\)
vì: \(\hept{\begin{cases}AMchung\\\widehat{BAM}=\widehat{MAC}\left(cmt\right)\end{cases}}\)
=> MD=ME
=> Trung điểm của canh đáy của tam giác cân cách đều 2 canh bên của tam giác
=> đpcm
Học tốt!!!!
đặt tam giác ABC cân tại A và có M là trung điểm của BC, tự vẽ hình nha
xét tam giác ABM và tam giác ACM có
AB=AC(gt)
ABC=ACB(gt)
BM=CM(gt)
=> tam giác ABM= tam giác ACM(cgc)
=>BAM=CAM( hai góc tương ứng)
=> AM là phân giác của BAC=> M thuộc tia phân giác của BAC
=> M cách đều hai cạnh bên của tam giác

c1:
gọi D là điểm trên cạnh đáy kéo dài BC của tam giác cân ABC.(D thuộc tia BC)
H, K là hình chiếu của D trên AB, AC .do tam giác ABC cân tại A suy ra DB là phân giác HDK (1)
gọi CP là đường cao của tam giác ABC.kẻ CQ vuông góc DH (2)
theo (1) và (2) ta suy ra điều phải chứng minh
C2:
từ B kẻ BP vuông góc DK, BH vuông góc AC (3)
từ (1) và (3) suy ra điều phải chứng minh

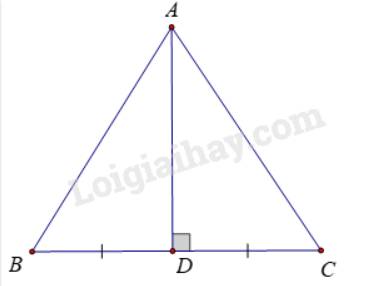
a) Kẻ đường trung trực của đoạn thẳng BC, cắt BC tại D
Ta có: Tam giác ABC cân nên AB = AC
\( \Rightarrow A\)thuộc đường trung trực của cạnh BC (t/c)
\( \Rightarrow AD\)là đường trung trực của BC.
Xét \(\Delta ABD\)và \(\Delta ACD\)có:
AB = AC (gt)
BD = CD (gt)
AD: cạnh chung
\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - c - c} \right)\)
\( \Rightarrow \widehat {BAD} = \widehat {CAD}\)
\( \Rightarrow \)AD là tia phân giác góc BAC.
Vậy tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b)
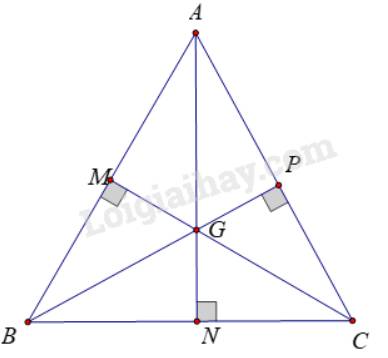
Ta có: Điểm cách đều ba đỉnh của tam giác là giao điểm ba đường trung trực của tam giác đó.
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại A có AN là đường trung tuyến
\( \Rightarrow \) AN là đường phân giác xuất phát từ đỉnh A (cm ở ý a)
Tương tự: BP, CM lần lượt là đường phân giác xuất phát từ B và C của tam giác ABC
Mà AN cắt BP tại G
\( \Rightarrow G\) là giao điểm ba đường phân giác của tam giác ABC
\( \Rightarrow G\) cách đều ba cạnh của tam giác ABC (Tính chất