OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
G
gfgfgrrgrgdrgfg
16 tháng 2 2018 - olm

chứng minh rằng :(|x|/28+|x|)+(|y|/28+|y|)=>|x-y|/28+|x-y| với mọi x,y

mọi người giúp mình với ,có trước chủ nhật thì càng tốt

 
#Toán lớp 7
0
T
TVT_Covippro
27 tháng 7 2020 - olm

Chứng minh rằng :

   a , với mọi x ,y thuộc Z thì [x+y]=[x]+[y]

   b,với x thuộc Z , y thuộc Q thì [x+y]=x+[y]

 *chú ý : [y] là phần nguyên của y
#Toán lớp 7
0
T
TVT_Covippro
26 tháng 7 2020 - olm

Chứng minh rằng :

   a , với mọi x ,y thuộc Z thì [x+y]=[x]+[y]

   b,với x thuộc Z , y thuộc Q thì [x+y]=x+[y]

 *chú ý : [y] là phần nguyên của y
#Toán lớp 7
4
AP
Ashes PK249
27 tháng 7 2020

\(a,\left|x+y\right|\ge0\)

     \(\left|x\right|+\left|y\right|\ge0\)\(\Rightarrow\left|x+y\right|=\left|x\right|+\left|y\right|\)

Đúng(0)
T
TVT_Covippro
27 tháng 7 2020

sai rồi

Đúng(0)
#𝒌𝒂𝒎𝒊ㅤ♪
16 tháng 2 2019 - olm

a) Cho hàm số y = f(x) = \(3x^2+2\). Chứng minh rằng với mọi x thì f(-x) = f(x)

b)Cho hàm số y= f(x) = \(4x^3-2x.\)Chứng minh rằng với mọi x thì f(-x) = -f(x)
#Toán lớp 7
2
T
tth_new
16 tháng 2 2019

a) \(y=f\left(x\right)=3\left(x^2+\frac{2}{3}\right)\)

\(f\left(-x\right)=3\left[\left(-x\right)^2+\frac{2}{3}\right]=f\left(x\right)^{\left(đpcm\right)}\)

b) Đề sai,thay x = 3 vào là thấy.

Đúng(0)
N3
Nguyên :3
16 tháng 2 2019

b (đè sai

Đúng(0)
PN
Phạm Nguyệt
15 tháng 6 2016 - olm

Chứng minh rằng với mọi x, y thuộc Q thì :

\(\left|x-y\right|\ge\left|x\right|-\left|y\right|\)
#Toán lớp 7
1
NH
Nguyễn Hoàng Tiến
15 tháng 6 2016

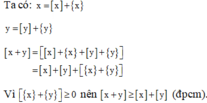
Ta có:

\(VT^2\ge VP^2\)

\(\left(\left|x-y\right|\right)^2\ge\left(\left|x\right|-\left|y\right|\right)^2\)

\(x^2+y^2-2xy\ge x^2+y^2-2\left|xy\right|\)

\(-2xy\ge-2\left|xy\right|\)

\(2xy\le2\left|xy\right|\)

Điều này đúng nên BĐT đúng

Đúng(0)
PN
Phạm Nguyệt
15 tháng 6 2016 - olm

Chứng minh rằng với mọi x, y thuộc Q thì : 

\(\left|x+y\right|\le\left|x\right|+\left|y\right|\)
#Toán lớp 7
1
TN
Tiểu Nghé
15 tháng 6 2016

đây là  1 trong những bất đẳng thức cơ bản bạn mua sách về mà tham khảo

Đúng(0)
1N
10-Nguyễn Thị Mỹ Hương
20 tháng 11 2021

chứng minh rằng B=xy(x^2-y^2)(x^2+y^2) chia hết cho 30 với mọi số nguyên x,y
#Toán lớp 7
0
PV
Phạm Văn Huy
28 tháng 4 2016 - olm

Bài 1. Chứng minh rằng với mọi x,y thuộc R thì

x.y +11+222+3333+.... thuộc z
#Toán lớp 7
0
TN
truong nhat linh
7 tháng 7 2018 - olm

Chứng minh rằng P = 2x ( x + y - 1 ) + y2 +1 luôn nhận giá trị không âm với mọi x , y
#Toán lớp 7
3
AK
Arima Kousei
7 tháng 7 2018

Ta có : 

\(P=2x\left(x+y-1\right)+y^2+1\)

\(\Rightarrow P=2x^2+2xy-2x+y^2+1\)

\(\Rightarrow P=\left(x^2+2xy+y^2\right)+\left(x^2-2x+1\right)\)

\(\Rightarrow P=\left(x+y\right)^2+\left(x-1\right)^2\ge0\forall xy\)

\(\RightarrowĐpcm\)

Đúng(0)
AK
Arima Kousei
7 tháng 7 2018

Công thức đây :

\(\left(a+b\right)^2=a^2+2ab+b^2\)

\(\left(a-b\right)^2=a^2-2ab+b^2\)

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP