
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()

Từ M kẻ MP ⊥ Ox, MQ ⊥ Oy
=> = cosα;
=
= sinα;
Trong tam giác vuông MPO:
MP2+ PO2 = OM2 => cos2 α + sin2 α = 1

Chọn C.
Ta có tan α – cotα = 1

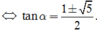
Do ![]() suy ra tanα < 0 nên
suy ra tanα < 0 nên
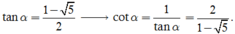
Thay
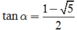 và
và 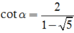
vào P ta được
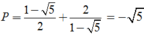

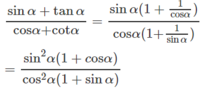
Vì 1 + cosα ≥ 0 và 1 + sinα ≥ 0 cho nên biểu thức đã cho không thể có giá trị là một số âm.

Trên đường tròn lượng giác,từ A(1,0) vẽ tiếp tuyến t’At với đường tròn lượng giác.
Từ B(0,1) vẽ tiếp tuyến s’Bs với đường tròn lượng giác .
Cho cung lượng giác AM có số đo α (α ≠ π/2 + kπ ). Gọi T là giao điểm của OM với trục t’At.
Gọi S là giao điểm của OM và trục s’Bs.
Khi β = α + kπ thì điểm cuối của góc β sẽ trùng với điểm T trên trục tan. Do đó
tan(α + kπ) = tanα.
Khi β = α + kπ thì điểm cuối của góc β sẽ trùng với điểm S trên trục cot. Do đó
cot(α + kπ) = cotα.

1 / ( sin 2 α ) = 1 + c o t 2 α = 1 + 4/9 = 13/9 ⇒ sin 2 α = 9 / 13 .
Suy ra sinα = ± 3 / 13 .
Vì π/2 < α < π nên sinα > 0. Vậy sinα = 3 / 13 . .
Từ đó cosα = sinα.cotα = ( - 2 ) / 13 .
Đáp án là A.