Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Mai Anh ơi đề bạn là tìm x với điều kiện ra sao phải rõ ràng chứ như vầy ai làm được 
Lời giải:
a)
Ta có: \(2^x-2^y=256=2^8\) (\(\Rightarrow x>y\) )
\(\Leftrightarrow 2^y(2^{x-y}-1)=2^8(*)\)
Vì \(x>y\Rightarrow x-y>0\Rightarrow 2^{x-y}\) chẵn. Do đó \(2^{x-y}-1\) lẻ. Kết hợp với
\((*)\Rightarrow 2^{x-y}-1=1\Leftrightarrow x-y=1\)
Khi đó: \(2^8=2^y(2^{x-y}-1)=2^y(2-1)=2^y\Rightarrow y=8\)
\(\Rightarrow x=y+1=9\)
PT có nghiệm \((x,y)=(9,8)\)
b) Giả sử \(x=y\Rightarrow 3^x+3^y= 2.3^x=3\vdots 2\) (vô lý). Do đó \(x\neq y\)
Không mất tính tổng quát giả sử \(x> y\).
PT tương đương: \(3^y(3^{x-y}+1)=3\) \((**)\)
Vì \(x>y\Rightarrow x-y\geq 1\Rightarrow 3^{x-y}\vdots 3\)
\(\Rightarrow 3^{x-y}+1\not\vdots 3\). Kết hợp với \((**)\Rightarrow 3^{x-y}+1=1\Leftrightarrow 3^{x-y}=0\) (vl)
Do đó PT vô nghiệm.
Câu c)
\((x-2)^2=3\Leftrightarrow \) \(\left[{}\begin{matrix}x-2=\sqrt{3}\\x-2=-\sqrt{3}\end{matrix}\right.\)
\(\Leftrightarrow \)\(\left[{}\begin{matrix}x=2+\sqrt{3}\\x=2-\sqrt{3}\end{matrix}\right.\)
Câu d)
Nếu \(y=0\Rightarrow 2007^x=2000-2008^0=1999\Rightarrow x\not\in\mathbb{N}\)
Nếu \(y\geq 1.\)Ta thấy với mọi số tự nhiên \(x\in\mathbb{N}\Rightarrow 2007^x\) lẻ và \(2008^y\) chẵn
\(\Rightarrow 2007^x+2008^y\) lẻ. Mà 2000 là số chẵn, do đó pt vô nghiệm.
Câu 2:
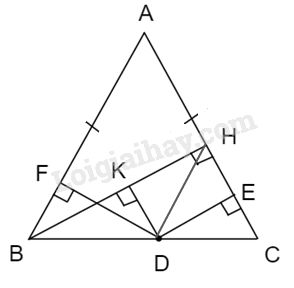
Kẻ \(DK\perp BH.\)
Mà \(BH\perp AC\left(gt\right)\)
=> \(DK\) // \(AC\) (từ vuông góc đến song song).
Hay \(DK\) // \(HC.\)
=> \(\widehat{KDB}=\widehat{HCD}\) (vì 2 góc đồng vị).
+ Vì \(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
=> \(\widehat{FBD}=\widehat{HCD}.\)
Mà \(\widehat{KDB}=\widehat{HCD}\left(cmt\right)\)
=> \(\widehat{FBD}=\widehat{KDB}.\)
Xét 2 \(\Delta\) vuông \(BFD\) và \(DKB\) có:
\(\widehat{BFD}=\widehat{DKB}=90^0\)
Cạnh BD chung
\(\widehat{FBD}=\widehat{KDB}\left(cmt\right)\)
=> \(\Delta BFD=\Delta DKB\) (cạnh huyền - góc nhọn).
=> \(DF=BK\) (2 cạnh tương ứng) (1).
Nối D với H.
+ Vì \(DK\) // \(AC\left(cmt\right)\)
=> \(DK\) // \(EH.\)
=> \(\widehat{KDH}=\widehat{EHD}\) (vì 2 góc so le trong).
Xét 2 \(\Delta\) vuông \(DEH\) và \(HKD\) có:
\(\widehat{DEH}=\widehat{HKD}=90^0\)
Cạnh DH chung
\(\widehat{EHD}=\widehat{KDH}\left(cmt\right)\)
=> \(\Delta DEH=\Delta HKD\) (cạnh huyền - góc nhọn).
=> \(DE=HK\) (2 cạnh tương ứng) (2).
Từ (1) và (2) => \(DF+DE=BK+HK.\)
Mà \(BK+HK=BH\)
=> \(DF+DE=BH\left(đpcm\right).\)
Chúc bạn học tốt!
Với những giá trị nguyên nào của X thì phân số sau tối giản:
x−82x−17x−82x−17
x−4x+1x−4x+1
10x+710x+7
x−1x2
cảm ơn vì câu trả lời của bạn bạn có thể giúp mình câu hỏi dưới đây ko ạ cảm ơn bạn rất nhiều
Tương tự, thay số vào là được :)
Câu hỏi của Đặng Quốc Vinh - Toán lớp 8 | Học trực tuyến
A B C O D E
a) Ta có: AD + DB = AB
AE + EC = AC
mà AB = AC; AD = AE => DB = EC
Vì AB = AC nên \(\Delta\)ABC cân tại A
=> \(\widehat{ABC}\) = \(\widehat{ACB}\) (góc đáy)
hay \(\widehat{DBC}\) = \(\widehat{ECB}\)
Xét \(\Delta\)DCB và \(\Delta\)EBC có:
DB = EC (c/m trên)
\(\widehat{DBC}\) = \(\widehat{ECB}\) (c/m trên)
BC chung
=> \(\Delta\)DCB = \(\Delta\)EBC (c.g.c)
=> DC = EB (2 cạnh tương ứng)
b) Do \(\Delta\)DCB = \(\Delta\)EBC (câu a)
=> \(\widehat{BDC}\) = \(\widehat{CEB}\) (2 góc t/ư)
hay \(\widehat{BDO}\) = \(\widehat{CEO}\)
Xét \(\Delta\)ABE và \(\Delta\)ACD có:
AE = AD (gt)
\(\widehat{A}\) chug
AB = AC (gt)
=> \(\Delta\)ABE = \(\Delta\)ACD (c.g.c)
=> \(\widehat{ABE}\) = \(\widehat{ACD}\) (2 góc t/ư)
hay \(\widehat{DBO}\) = \(\widehat{ECO}\)
Xét \(\Delta\)BOD và \(\Delta\)COE có:
\(\widehat{DBO}\) = \(\widehat{ECO}\) (c/m trên)
BD = CE (c/m trên)
\(\widehat{BDO}\) = \(\widehat{CEO}\) (c/m trên)
=> \(\Delta\)BOD = \(\Delta\)COE (g.c.g)
D E A B C O 1 2 1 2 1 1
a, xét \(\Delta\) ABE và \(\Delta\) ACD có
\(\widehat{A}\) góc chung
AE = AD (gt)
AB = AC (gt)
=> \(\Delta\) ABE = \(\Delta\) ACD (cgc) => BE = CD
b, ta có \(\widehat{D1}\) + \(\widehat{D2}\) = 180o ( kề bù )
\(\widehat{E1}\) + \(\widehat{E2}\) = 180o ( kề bù )
mà \(\widehat{D1}\) = \(\widehat{E1}\) ( \(\Delta\) ABE = \(\Delta\) ACD )
=> \(\widehat{D2}\) = \(\widehat{E2}\)
ta có AD + DB = AB
AE + EC = AC
mà AB = AC, AD = AE => DB = EC
xét Δ BOD và Δ COE có
\(\widehat{D2}\) = \(\widehat{E2}\)
Ta có: \(\left(3^{n+2}+3^n\right)-\left(2^{n+2}+2^n\right)\)
=> \(3^n\left(3^2+1\right)-2^n\left(2^2+1\right)\)
=> \(3^n.10-2^n.5\)
=> \(3^n.10-2^{n-1}.10\)
=> \(10.\left(3^n-2^{n-1}\right)\)
Mà 10 ⋮ 10 => \(3^n-2^{n-1}\) ⋮ 10
=>\(3^{n+2}-2^{n+2}+3^n-2^n\) ⋮ 10
sai sót thì thông cảm nha
nếu đúng thì tick nhé
thanks