Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do a;b;c là độ dài 3 cạnh của tam giác
\(\Rightarrow abc\ge\left(a+b-c\right)\left(b+c-a\right)\left(a+c-b\right)\)
\(\Leftrightarrow4\left(a^3+b^3+c^3\right)+15abc\ge\left(a+b+c\right)^3\)
\(\Leftrightarrow3\left(a^3+b^3+c^3\right)+\dfrac{45}{4}abc\ge\dfrac{3}{4}\left(a+b+c\right)^3\)
\(\Rightarrow3\left(a^3+b^3+c^3\right)+4abc\ge\dfrac{3}{4}\left(a+b+c\right)^3-\dfrac{29}{4}abc\)
Do đó ta chỉ cần chứng minh:
\(\dfrac{3}{4}\left(a+b+c\right)^3-\dfrac{29}{4}abc\ge\dfrac{13}{27}\left(a+b+c\right)^3\)
\(\Leftrightarrow\left(a+b+c\right)^3\ge27abc\) (hiển nhiên đúng theo AM-GM)

a/ \(\overrightarrow{AC}=3\overrightarrow{AM};\overrightarrow{BN}=\frac{1}{2}\overrightarrow{BC}\)
\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{BN}=\frac{1}{3}\overrightarrow{CA}+\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BC}\)
\(=\frac{1}{3}\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CD}+\overrightarrow{DC}+\frac{1}{2}\overrightarrow{BC}=\frac{2}{3}\overrightarrow{DC}+\frac{1}{6}\overrightarrow{BC}=\frac{2}{3}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{BA}+\frac{1}{6}\overrightarrow{AC}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}\)
Hmm, MN làm sao vuông góc vs BC đc. Nó chỉ vuông góc khi M là TĐ của AC thôi, bởi N là trung điểm của BC rồi mà, hại não :((
2/\(\overrightarrow{BK}=\frac{4}{13}\overrightarrow{BA}\Rightarrow\overrightarrow{BC}+\overrightarrow{CK}=\frac{4}{13}\overrightarrow{BC}+\frac{4}{13}\overrightarrow{CA}\)
\(\Leftrightarrow\overrightarrow{CK}=\frac{9}{13}\overrightarrow{CB}+\frac{4}{13}\overrightarrow{CA}\)
\(\overrightarrow{GB}+\overrightarrow{GM}+\overrightarrow{GN}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GC}+\overrightarrow{CB}+\overrightarrow{GC}+\overrightarrow{CM}+\overrightarrow{GC}+\overrightarrow{CN}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{GC}+\overrightarrow{CB}+\overrightarrow{CN}+\overrightarrow{NM}+\overrightarrow{CN}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{GC}+\overrightarrow{CB}+2\overrightarrow{CN}+\frac{1}{2}\overrightarrow{BA}+\frac{1}{6}\overrightarrow{CA}=\overrightarrow{0}\)
Ta có : \(\overrightarrow{CN}=\frac{1}{2}\overrightarrow{CB}\Rightarrow3\overrightarrow{GC}+\overrightarrow{CB}+\overrightarrow{CB}+\frac{1}{2}\overrightarrow{BA}+\frac{1}{6}\overrightarrow{CA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{CG}=\frac{2}{3}\overrightarrow{CB}+\frac{1}{6}\overrightarrow{BA}+\frac{1}{18}\overrightarrow{CA}\)
\(\Leftrightarrow\overrightarrow{CG}=\frac{2}{3}\overrightarrow{CB}+\frac{1}{6}\overrightarrow{BC}+\frac{1}{6}\overrightarrow{CA}+\frac{1}{18}\overrightarrow{CA}\)
\(=\frac{1}{2}\overrightarrow{CB}+\frac{2}{9}\overrightarrow{CA}\)
Có \(\overrightarrow{CK}=\frac{18}{13}\overrightarrow{CG}\Rightarrow\) C,G,K thẳng hàng

\(a^3+a\ge2a^2\) ; \(b^3+b\ge2b^2\); \(c^3+c\ge2c^2\)
\(\Rightarrow a^3+b^3+c^3+3\ge2\left(a^2+b^2+c^2\right)\)
\(\Rightarrow a^3+b^3+c^3+ab+ac+bc\ge2\left(a^2+b^2+c^2\right)+ab+ac+bc-3\)
Mặt khác
\(P=2\left(a^2+b^2+c^2\right)+ab+ac+bc-3=\frac{3}{2}\left(a^2+b^2+c^2\right)+\frac{1}{2}\left(a+b+c\right)^2-3\)
\(P=\frac{3}{2}\left(a^2+b^2+c^2\right)+\frac{3}{2}\ge\frac{3}{2}.\frac{\left(a+b+c\right)^2}{3}+\frac{3}{2}=6\)
\(\Rightarrow a^3+b^3+c^3+ab+ac+bc\ge6\)
Dấu "=" xảy ra khi \(a=b=c=1\)

Áp dụng bất đẳng thức Cô – si ta có:
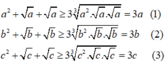
Cộng vế với vế bất phương trình (1), (2), (3) ta được:
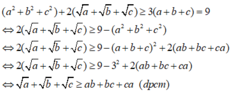

Lời giải:
Do $a+b+c=1$ nên:
\(\text{VT}=\sqrt{\frac{ab}{c(a+b+c)+ab}}+\sqrt{\frac{bc}{a(a+b+c)+bc}}+\sqrt{\frac{ca}{b(a+b+c)+ac}}\)
\(=\sqrt{\frac{ab}{(c+a)(c+b)}}+\sqrt{\frac{bc}{(a+b)(a+c)}}+\sqrt{\frac{ca}{(b+c)(b+a)}}\)
Áp dụng BĐT AM-GM:
\(\sqrt{\frac{ab}{(c+a)(c+b)}}\leq \frac{1}{2}\left(\frac{a}{c+a}+\frac{b}{c+b}\right)\)
\(\sqrt{\frac{bc}{(a+b)(a+c)}}\leq \frac{1}{2}\left(\frac{b}{a+b}+\frac{c}{c+a}\right)\)
\(\sqrt{\frac{ca}{(b+c)(b+a)}}\leq \frac{1}{2}\left(\frac{c}{b+c}+\frac{a}{b+a}\right)\)
Cộng theo vế:
\(\Rightarrow \text{VT}\leq \frac{1}{2}\left(\frac{a+b}{a+b}+\frac{b+c}{b+c}+\frac{c+a}{c+a}\right)=\frac{3}{2}\) (đpcm)
Dấu "=" xảy ra khi $a=b=c=\frac{1}{3}$

1) \(a^5-a=a\left(a^4-1\right)=a\left(a^2-1\right)\left(a^2+1\right)\)
\(=\left(a-1\right)a\left(a+1\right)\left(a^2-4+5\right)\)
\(=\left(a-1\right)a\left(a+1\right)\left(a^2-4\right)+5\left(a-1\right)a\left(a+1\right)\)
\(=\left(a-2\right)\left(a-1\right)a\left(a+1\right)\left(a+2\right)+5\left(a-1\right)a\left(a+1\right)⋮5\)
Vì \(\left(a-2\right)\left(a-1\right)a\left(a+1\right)\left(a+2\right)⋮5\)( tích 5 số nguyên liên tiếp chia hết cho 5)
và \(5\left(a-1\right)a\left(a+1\right)⋮5\)
=> \(a^5-a⋮5\)
Nếu \(a^5⋮5\)=> a chia hết cho 5

\(VT=\dfrac{a^4}{ab}+\dfrac{b^4}{bc}+\dfrac{c^4}{ca}\ge\dfrac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ca}\ge\dfrac{\left(ab+bc+ca\right)^2}{ab+bc+ca}=ab+bc+ca\)
Dấu "=" xảy ra khi \(a=b=c\)
Ta chứng minh bđt phụ \(x^2+y^2+z^2\ge xy+yz+zx\forall x,y,z>0\)
\(\Leftrightarrow2x^2+2y^2+2z^2\ge2xy+2yz+2zx\Leftrightarrow x^2-2xy+y^2+y^2-2yz+z^2+z^2-2zx+x^2\ge0\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\)\(\Rightarrow x^2+y^2+z^2\ge xy+yz+zx\left(1\right)\)
Áp dụng bđt Cô-si vào các số a,b,c dương :
\(\dfrac{a^3}{b}+ab\ge2\sqrt{\dfrac{a^3}{b}\cdot ab}=2\sqrt{a^4}=2a^2\)
Chứng minh tương tự ta được:
\(\dfrac{b^3}{c}+bc\ge2b^2;\dfrac{c^3}{a}+ca\ge2c^2\)
\(\Rightarrow\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}+ab+bc+ca\ge2a^2+2b^2+2c^2\ge2ab+2bc+2ca\) (do áp dụng (1)) \(\Rightarrow\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}\ge2\left(ab+bc+ca\right)-\left(ab+bc+ca\right)=ab+bc+ca\)
Dấu = xảy ra \(\Leftrightarrow a=b=c\)