Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn trả lời:
Trong phương trình biểu diễn các đường thẳng (k + 1)x – 2y = 1, ta nhận thấy: Khi x = 0 thì
Điều này chứng tỏ rằng các đường thẳng có phương trình:
(k + 1)x – 2y = 1 luôn luôn đi qua điểm cố định I có tọa độ (0;−12)∀k∈R

Giả sử đường thẳng (k + 1)x – 2y = 1 đi qua điểm cố định M(x0; y0)
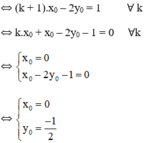
Vậy điểm cố định mà đường thẳng (k + 1)x – 2y = 1 đi qua là 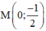
chứng minh rằng khi k thay đổi các đường thẳng (k+1)x-2y=1 luôn đi qua một điểm cố định. tìm điển đó

Giải:
Trong phương trình biểu diễn các đường thẳng \(\left(k+1\right)x-2y=1\) ta nhận thấy:
Khi \(x=0\) thì:
Điều này chứng tỏ rằng các đường thẳng có phương trình:
\(\left(k+1\right)x-2y=1\) luôn luôn đi qua điểm cố định I có tọa độ \(\left(0;\frac{1}{2}\right)\forall k\in R\)


Gọi điểm cố định mà các đường thẳng (d) đều đi qua P( x o , y o ).
Ta có:
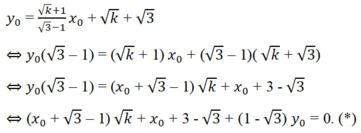
Phương trình (*) nghiệm đúng với mọi giá trị không âm của k , do đó ta có:
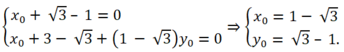
Vậy, với k ≥ 0, các đường thẳng (d) đều đi qua điểm cố định P(1- 3 ; 3 – 1).

Với k ≥ 0 ta có:
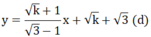
Giả sử ( x 0 ; y 0 ) là điểm cố định mà (d) luôn đi qua
Khi đó ta có:
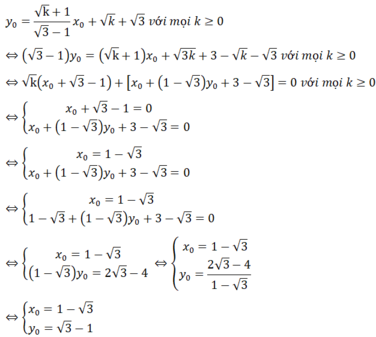
Vậy điểm cố định mà (d) luôn đi qua với mọi k ≥ 0 là (1- 3 ; 3 -1)
Giả sử đường thẳng (k + 1)x – 2y = 1 đi qua điểm cố định M ( x 0 ; y 0 )
Vậy điểm cố định mà đường thẳng (k + 1)x – 2y = 1 đi qua là