Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đặt \(f\left(x\right)=x^n+\left(m+1\right)x-1\)
Hàm \(f\left(x\right)\) liên tục trên R
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=\lim\limits_{x\rightarrow-\infty}\left(x^n-\left(m+1\right)x-1\right)=\lim\limits_{x\rightarrow-\infty}x^n\left(1-\dfrac{m+1}{x^{n-1}}-\dfrac{1}{x^n}\right)=-\infty< 0\)
\(\Rightarrow\) Luôn tồn tại một số thực \(a< 0\) sao cho \(f\left(a\right)< 0\)
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow+\infty}x^n\left(1-\dfrac{m+1}{x^{n-1}}-\dfrac{1}{x^n}\right)=+\infty>0\)
\(\Rightarrow\) Luôn tồn tại một số thực \(b>0\) sao cho \(f\left(b\right)>0\)
\(\Rightarrow f\left(a\right).f\left(b\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm trên (a;b) hay pt đã cho luôn luôn có nghiệm
Hàm số f ( x ) = x n + a 1 x n - 1 + a 2 x n - 2 + . . . + a n - 1 x + a n = 0 xác định trên R
- Ta có
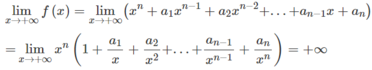
Vì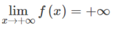 
nên với dãy số
(
x
n
)
bất kì mà
x
n
→
+
∞
ta luôn có lim
f
(
x
n
)
=
+
∞
Do đó, f ( x n ) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì f ( x n ) > 1 kể từ một số hạng nào đó trở đi.
Nói cách khác, luôn tồn tại số a sao cho f(a) > 1 (1)
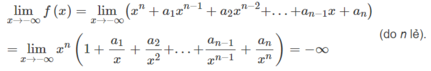
Vì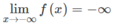 
nên với dãy số
(
x
n
)
bất kì mà
x
n
→
−
∞
ta luôn có lim
f
(
x
n
)
=
−
∞
hay
l
i
m
[
−
f
(
x
n
)
]
=
+
∞
Do đó, − f ( x n ) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì − f ( x n ) > 1 kể từ số hạng nào đó trở đi. Nói cách khác, luôn tồn tại b sao cho −f(b) > 1 hay f(b) < −1 (2)
- Từ (1) và (2) suy ra f(a).f(b) < 0
Mặt khác, f(x) hàm đa thức liên tục trên R nên liên tục trên [a; b]
Do đó, phương trình f(x) = 0 luôn có nghiệm.
Mình nhầm \(C^1_{2016}a_{2015}\)thành \(C^1_{2016}a^{2015}\)
Xét \(x\ne1\)
\(\left(1+x+...+x^{10}\right)^{11}=a_0+a_1x+...+a_{110}x^{110}\)
\(\Leftrightarrow\left(x-1\right)^{11}\left(1+x+...+x^{10}\right)^{11}=\left(x-1\right)^{11}\left(a_1+a_1x+...+a_{110}x^{110}\right)\)
\(\Leftrightarrow\left(x^{11}-1\right)^{11}=\left(x-1\right)^{11}\left(a_0+a_1x+...+a_{110}x^{110}\right)\)
\(VP=\left(x-1\right)^{11}\left(a_0+a_1x+...\right)=\left(\sum\limits^{11}_{k=0}C_{11}^kx^k\left(-1\right)^{11-k}\right)\left(a_0+a_1x+...\right)\) (1)
Ta thấy tổng các hệ số của \(x^{11}\) trong khai triển (1) là:
\(C_{11}^0\left(-1\right)^{11}.a_{11}+C_{11}^1\left(-1\right)^{10}a_{10}+C_{11}^2\left(-1\right)^9a_9+...+C_{11}^{11}\left(-1\right)^0a_0\)
\(=-C_{11}^0a_{11}+C_{11}^1a_{10}-C_{11}^2a_9+...+C_{11}^{11}a_0=-T\)
\(VT=\sum\limits^{11}_{k=0}C_{11}^k\left(x^{11}\right)^k.\left(-1\right)^{11-k}\)
Hệ số của \(x^{11}\) trong khai triển trên là \(C_{11}^1\left(-1\right)^{10}=C_{11}^1=11\)
Mà \(VT=VP\Rightarrow-T=11\Rightarrow T=-11\)
a. Cho \(x=1\) ta được:
\(\left(1+1+2\right)^{10}=a_0+a_1+a_2+...+a_{20}\)
\(\Rightarrow S_1=4^{10}\)
b. Cho \(x=2\) ta được:
\(\left(1+2+8\right)^{10}=a_0+a_1.2+a_2.2^2+...+a_{20}.2^{20}\)
\(\Rightarrow S_2=11^{10}\)
c.
\(\left(1+x+2x^2\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^k\left(x+2x^2\right)^k=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^kC_k^i.2^ix^{i+k}\)
Số hạng chứa \(\Rightarrow\left\{{}\begin{matrix}i+k=17\\0\le i\le k\le10\end{matrix}\right.\)
\(\Rightarrow\left(i;k\right)=\left(7;10\right);\left(8;9\right)\)
\(\Rightarrow a_{17}=C_{10}^{10}C_{10}^7.2^7+C_{10}^9.C_9^8.2^8=...\)
Tham khảo: