K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
G
30 tháng 1 2022
a: \(3x^2+y^2+10x-2xy+26=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(2x^2+10x+\dfrac{5}{2}\right)+\dfrac{47}{2}=0\)
\(\Leftrightarrow\left(x-y\right)^2+2\cdot\left(x+\dfrac{5}{2}\right)^2+\dfrac{47}{2}=0\)(vô lý)
b: \(\Leftrightarrow3x^2-12x+12+6y^2-20y+\dfrac{50}{3}+\dfrac{34}{3}=0\)
\(\Leftrightarrow3\left(x-2\right)^2+6\left(y-\dfrac{5}{3}\right)^2+\dfrac{34}{3}=0\)(vô lý)
HA
Bài 1: Chứng minh rằng: Nếu tam giác có hai đường phân giác bằng nhau thì tam giác đó là tam giác cân.
Bài 2: Nếu 33 cạnh của một tam giác thoả mãn cc là độ dài cạnh nhỏ nhất...
Đọc tiếp
Bài 1: Chứng minh rằng: Nếu tam giác có hai đường phân giác bằng nhau thì tam giác đó là tam giác cân.
Bài 2: Nếu
#Hỏi cộng đồng OLM
#Toán lớp 8
1
5 tháng 3 2018
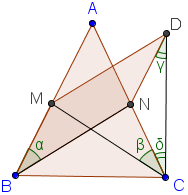
gọi 2 đường phân giác trong BN, CM bằng nhau
dựng hình bình hành BMDN và kí hiệu các góc α,β,γ,δα,β,γ,δ như hình vẽ
tam giác CMD cân tại M nên α+γ=β+δα+γ=β+δ (1)
nếu α>βα>β thì xét hai tam giác BCN và CBM có BC chung, BN=CM,CBNˆ>BCMˆ⇒CN>BMBN=CM,CBN^>BCM^⇒CN>BM
mà BM=ND⇒γ>δ⇒α+γ>β+δBM=ND⇒γ>δ⇒α+γ>β+δ, mâu thuẫn với (1)
tương tự, ko thể xảy ra trường hợp α<βα<β
suy ra α=βα=β, đpcm
MD
Đoán tuổi
Bạn hãy lấy tuổi của mình:
- Cộng thêm 22;
- Lấy kết quả trên cộng với 55;
- Đọc kết quả cuối cùng sau khi đã trừ đi...
Đọc tiếp
Đoán tuổi
Bạn hãy lấy tuổi của mình:
- Cộng thêm #Hỏi cộng đồng OLM #Toán lớp 8
1
3 tháng 6 2019
Giả sử tuổi bạn là x. Đem tuổi của mình:
+ Cộng thêm 5 ta được x+5
+ Được bao nhiêu đem nhân với 2 ta được (x+5).2
+ Lấy kết quả trên cộng với 10 ta được (x+5).2+10
+ Nhân kết quả vừa tìm được với 5 ta được [(x+5).2+10].5
+ Đọc kết quả cuối cùng sau khi đã trừ đi 100 ta được
[(x+5).2+10].5–100
Rút gọn biểu thức trên:
\(\left[\left(x+5\right).2+10\right].5-100\)
=(2x+10+10).5−100
=(2x+20).5−100
=10x+100−100
=10x
Thực chất kết quả cuối cùng được đọc lên chính là 10 lần số tuổi của bạn
Vì vậy, khi đọc kết quả cuối cùng, thì tôi chỉ việc bỏ đi một chữ số 0 ở tận cùng là ra số tuổi của bạn. Chẳng hạn bạn đọc là 130 thì tuổi của bạn là 13.
Chúc bạn học tốt
HV
Cho số nguyên tố nn sao cho trong cách viết thập phân của số 20 chữ số. CMR trong...
Đọc tiếp
Cho số nguyên tố #Hỏi cộng đồng OLM #Toán lớp 8
0
V
n5−n=n(n4−1)=n(n2−1)(n2+1)n5−n=n(n4−1)=n(n2−1)(n2+1)
=n(n−1)(n+1)(n2−4+5)=n(n−1)(n+1)(n2−4+5)
=n(n−1)(n+1)(n2−4)+5n(n−1)(n+1)=n(n−1)(n+1)(n2−4)+5n(n−1)(n+1)
=n(n−1)(n+1)(n−2)(n+2)=n(n−1)(n+1)(n−2)(n+2)+5n(n−1)(n+1)5n(n−1)(n+1)
--Vì n(n+1)(n+2)(n−2)(n−1)n(n+1)(n+2)(n−2)(n−1)là tích của 5 số nguyên liên tiếp
=> n(n−1)(n+1)(n−2)(n+2)n(n−1)(n+1)(n−2)(n+2) chia hết cho 2;3;5
=> n(n−1)(n+1)(n−2)(n+2)n(n−1)(n+1)(n−2)(n+2) chia hết cho 30 (*)
-- vì n(n−1)(n+1)n(n−1)(n+1) là tích của 3 số nguyên liên tiếp
⇒n(n−1)(n+1)⇒n(n−1)(n+1) chia hết cho 2; 3
⇒n(n−1)(n+1)⋮6⇒n(n−1)(n+1)⋮6
=> 5n(n−1)(n+1)⋮5.6=305n(n−1)(n+1)⋮5.6=30 (**)
từ * và ** => n(n−1)(n+1)(n−2)(n+2)+5n(n−1)(n+1)⋮30n(n−1)(n+1)(n−2)(n+2)+5n(n−1)(n+1)⋮30
hay n5−n⋮30(đpcm)
like nhoa !!