Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
chứng minh trong 1 tam giác vuông lập phương cạnh huyền thì lớn hơn tổng lập phương 2 cạnh góc vuông

ờ thì..........................................................................................................................................................................................., dễ mà

C B A
Theo đề ra ta phải so sánh:
\(BC^3\)Và \(AB^3+AC^3\)
ta có:
\(BC^3=BC^2.BC\)
\(AB^3+AC^3=AB^2.AB+AC^2.AC\)
Theo định lí Pi-ta-go
Bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông
=>\(BC^2=AB^2+AC^2\)(1)
mà theo bất đẳng thức tam giác thì tổng 2 cạnh bất kì lớn hơn cạnh còn lại
=>\(AB+AC>BC\)(2)
Từ (1) và (2) \(\Rightarrow AB^3+AC^3>BC^3\)

Gọi x là dộ dài cạnh góc vuông thứ nhất (x < 20)
=> độ dài cạnh góc vuông thứ hai : 48 - 20 -x =28 - x
Theo đề bài ta có pt:
x2 + (28 -x)2 =202 (giải pt tìm x)

Tứ giác ABCD có AC vuông góc BD và AC cắt BD tạo O
\(AB^2=0A^2+OB^2\)
\(CD^2=OC^2+OD^2\)
\(AD^2=OA^2+OD^2\)
\(BC^2=OB^2+OC^2\)
\(\Rightarrow AB^2+CD^2=OA^2+OB^2+OC^2+OD^2\)(1)
\(AD^2+BC^2=OA^2+OD^2+OB^2+OC^2\)(2)
Từ (1) và 92) \(\Rightarrow AB^2+CD^2=AD^2+BC^2\)

Gọi giao của AC và BD là O , do hai đường chéo vuông góc
=> các tam giác : OAB, OBC, OCD, ODA là các tam giác vuông tại O
xét tam giác OAB có AB^2 = OA^2 + OB^2 (1)
xét tam giác ODC có DC^2 = OD^2 + OC^2 (2)
xét tam giác OAD có AD^2 = OA^2 + OD^2 (3)
xét tam giác OBC có BC^2 = OC^2 + OB^2 (4)
từ (1) và (2)=> AB^2 + CD^2 = OA^2 +OB^2 +OC^2 +OD^2 (5)
từ (3) và (4)=> BC^2 + AD^2 = OA^2 +OB^2 +OC^2 +OD^2 (6)
từ (5) và (6) => AB^2 + CD^2 = BC^2 + AD^2 ( dpcm )
Mình làm đúng không các bạn ??? Đúng thì nha !!

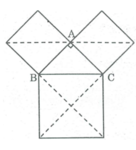
Gọi S là diện tích của tam giác ABC.
Hình vuông có cạnh AB được chia thành hai tam giác vuông cân bằng △ ABC nên diện tích hình vuông cạnh AB bằng 2S.
Hình vuông có cạnh AC được chia thành hai tam giác vuông cân bằng △ ABC nên diện tích hình vuông cạnh AC bằng 2S.
Hình vuông cạnh BC được chia thành bốn hình tam giác vuông cân bằng △ ABC nên có diện tích bằng 4S.
Vì 4S = 2S + 2S nên diện tích hình vuông dựng trên cạnh huyền bằng tổng diện tích hai hình vuông dựng trên hai cạnh góc vuông.