Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
+ Tổng các góc trong của 1 tam giác là 360 độ => Tứ giác có 3 góc vuông thì góc còn lại = 360-3.90=90 độ => tứ giác là HCN (Tứ giác có 4 góc vuông)
+ Giải sử có hình thang cân ABCD (AB<CD) và ^A=90 => ^B=90 (góc ở đáy)
Ta có AB//CD => ^D=180-^A=180-90=90 (Hai góc trong cùng phía bù nhau)
=> ^C=180-^B=180-90=90 (hai góc trong cùng phía bù nhau)
=> ^A=^B=^C=^D=90 => ABCD là hình chữ nhật
+ Hình bình hành có 1 góc vuông cũng áp dụng tính chất hai góc trong cùng phía bù nhau để c/m
Câu 13: Chọn câu đúng
A. Hình bình hành có hai đường chéo vuông góc là hình vuông B. Hình chữ nhật có hai đường chéo bằng nhau là hình vuông
C. Hình bình hành có hai đường chéo vuông góc là hình chữ nhật
D. Hình bình hành có một góc vuông là hình chữ nhật
Câu 14: Chọn câu sai
A. Hình bình hành có hai đường chéo vuông góc là hình thoi
B. Hình chữ nhật có hai đường chéo vuông góc là hình vuông
C. Tứ giác có hai cạnh đối bằng nhau là hình bình hành
D. Hình bình hành có hai cạnh kề bằng nhau là hình thoi
a) Nối AC
tam giác ACD có HA=HD; GC=GD nên HG là đường trung bình của tam giác ACD
=> HG//AC; HG=1/2AC. (1)
Tam giác ABC có EA=EB; FB=FC nên EF là đường trung bình của tam giác ABC
=> EF//AC; EF=1/2AC. (2)
Từ (1) và (2) suy ra HG//EF; HG=EF
Tứ giác EFGH có HG//EF; HG=EF
Vậy EFGH là hình bình hành.
b)* Để hình bình hành EFGH là hình thoi, ta cần có thêm hai cạnh kề bằng nhau.
Giả sử EH=FH mà EH=1/20BD(EA=EB, HA=HD nên EH là đường trung bình của tam giác ABD).
HG=1/2AC(cmt)
nên BD=AC
Vậy để hình bình hành EFGH trở thành hình thoi thì hai đường chéo AC và BD của tứ giác ABCD phải bằng nhau.
* Để hình bình hành EFGH là hình chữ nhật, ta cần có thêm một góc vuông.
Giả sử góc H=90 độ, vì HG//AC(cmt)
HG vuông góc với HE
từ hai điều này suy ra AC cũng vuông góc với HE
lại có HE//BD(cmt)
từ hai điều này lại suy ra AC vuông góc với BD
vậy để hình bình hành EFGH là hình thoi, hai đuognừ chéo AC và BD của tứ giác ABCD phải vuông góc với nhau.
* Để hình bình hành EFGH trở thành hình vuông ta cần có thêm hai cạnh kề bằng nhau và một góc vuông.
Giả sử HE=HG => AC=BD(cmt)
H=90 độ => AC vuông góc với BD(cmt)
vậy để hình bình hành EFGH là hình vuông, hai đuognừ chéo AC và BD của tứ giác ABCD phải bằng nhau và vuông góc với nhau.
Cách của tớ giống việt anh
a) Nối AC
tam giác ACD có HA=HD; GC=GD nên HG là đường trung bình của tam giác ACD
=> HG//AC; HG=1/2AC. (1)
Tam giác ABC có EA=EB; FB=FC nên EF là đường trung bình của tam giác ABC
=> EF//AC; EF=1/2AC. (2)
Từ (1) và (2) suy ra HG//EF; HG=EF
Tứ giác EFGH có HG//EF; HG=EF
Vậy EFGH là hình bình hành.
b)* Để hình bình hành EFGH là hình thoi, ta cần có thêm hai cạnh kề bằng nhau.
Giả sử EH=FH mà EH=1/20BD(EA=EB, HA=HD nên EH là đường trung bình của tam giác ABD).
HG=1/2AC(cmt)
nên BD=AC
Vậy để hình bình hành EFGH trở thành hình thoi thì hai đường chéo AC và BD của tứ giác ABCD phải bằng nhau.
* Để hình bình hành EFGH là hình chữ nhật, ta cần có thêm một góc vuông.
Giả sử góc H=90 độ, vì HG//AC(cmt)
HG vuông góc với HE
từ hai điều này suy ra AC cũng vuông góc với HE
lại có HE//BD(cmt)
từ hai điều này lại suy ra AC vuông góc với BD
vậy để hình bình hành EFGH là hình thoi, hai đuognừ chéo AC và BD của tứ giác ABCD phải vuông góc với nhau.
* Để hình bình hành EFGH trở thành hình vuông ta cần có thêm hai cạnh kề bằng nhau và một góc vuông.
Giả sử HE=HG => AC=BD(cmt)
H=90 độ => AC vuông góc với BD(cmt)
vậy để hình bình hành EFGH là hình vuông, hai đuognừ chéo AC và BD của tứ giác ABCD phải bằng nhau và vuông góc với nhau.
1.Định nghĩa
Tứ giác ABCD trên hình có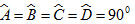
là một hình chữ nhật.
Tứ giác ABCD là hình chữ nhật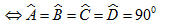
1. Chứng minh rằng hình chữ nhật ABCD trên hình 84 cũng là một hình bình hành, một hình thang cân.
Từ định nghĩa hình chữ nhật, ta suy ra: Hình chữ nhật cũng là một hình bình hành, cũng là một hình thang cân.
2. Tính chất
Hình chữ nhật có tất cả các tính chất của hình bình hành, của hình thang cân.
Từ tính chất của hình thang cân và hình bình hành, ta có:
3. Dấu hiệu nhận biết
Sau đây ta chứng minh dấu hiệu nhận biết 4, các dấu hiệu còn lại bạn tự chứng minh.
Giả thiết : ABCD là hình bình hành, AC = BD.
Kết luận : ABCD là hình chữ nhật
Chứng minh :
ABCD là hình bình hành nên AB // CD, AD // BC.
Bạn thêm hình vẽ nữa nha !
Ta có thể xét 2 tam giác bằng nhau để chứng minh .
Không chắc cho lắm .