

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Giả sử hình thang là ABCD,
Qua B kẻ đường thẳng với AC cắt DC tại E
a)Ta có ACD=BAC (AB//CD)
mà ACD =BEC =>BEC=BAC
Xét tam giac ABC va tam giác ECB
+BC chung
+ACB=EBC(so le trong)
+BEC=BAC(cm trên )
=>tam giac ABC =tam giac ECB
=>BDC=BEC
mà BEC=ACD(đồng vị)=>ACD=BDC
xét tam giac ACD va tam giac BDC,ta có :
+DC chung
+ACD=BDC
+AC=BD(gt)
=>tam giac ACD=tam giác BDC
=>ADC=BCD
=>ABCD la hình thang cân (dfcm)

Xét hình thang ABCD có các đường cao AH và BK. Từ A kẻ đường thẳng song song với BD cắt CD ở E Þ AB = ED.
Chứng minh A C H ^ = 45 0 . Do DEAC vuông cân ở A nên A H = C H = E H = A B + C D 2

Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E.
Ta có:
Góc ACD = góc BED (tính chất góc hình bình hành)
mà gócBDE = gócBED ( BDE là tam giac cân tại B)
=> góc ACD= góc BDC
xét 2 tam giác ACD và tam giác BDC có:
+ AC = BD ( gt)
+ góc ACD = góc BDC
+có cùng cạnh CD
=> tam giác ACD = tam giác BDC ( cạnh,góc,cạnh)
xét hình thang ABCD:
AD = BC vì tam giác ACD = tam giác BDC
=> ABCD là hình thang cân.
Vậy hình thang có hai đường chéo bằng nhau là hình thang cân.(đpcm)

c/m bai` nay` như sau:goi hi`nh thang la ABCD,qua B kẻ đuong thẳng //với AC cắt DC tại E
a)đâu tiên em chứng minh tam giac BDE la tam giac cân tại B:ta co ACD=BAC(AB//CD)
ma` ACD =BEC =>BEC=BAC
xet tam giac ABC va tam giác ECB
+BC chung
+ACB=EBC(so le trong)
+BEC=BAC(cm trên )
=>tam giac ABC =tam giac ECB
=>BDC=BEC
ma `BEC=ACD(đồng vị)=>ACD=BDC
xét tam giac ACD va tam giac BDC,ta có :
+DC chung
+ACD=BDC
+AC=BD(gt)
=>tam giac ACD=tam giác BDC
=>ADC=BCD
=>ABCD la hi`nh thang cân (dfcm)
Chuc bạn học tốt!!!!

A B C D E 1 1
Kẻ BE // AC (\(E \in DC\))
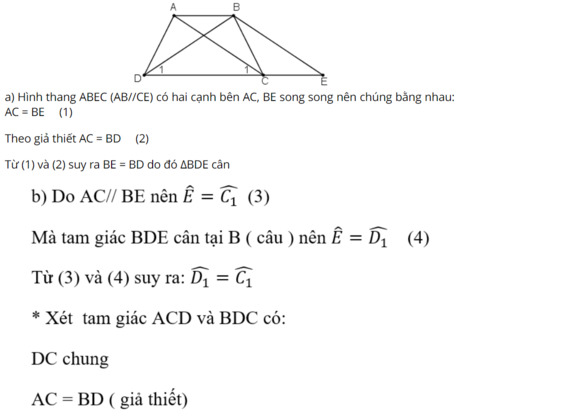
Hình thang ABEC (AB // CE) có 2 cạnh bên BE // AC.
=> BE = AC.
Mà AC = BD.
=> BE = BD.
=> ΔBDE cân tại B.
=> \(\widehat{D_1}=\widehat{E}\) (1)
Ta có: BE // AC (cách vẽ)
=> \(\widehat{C_1}=\widehat{E}\) (đồng vị)
Từ (1) và (2) suy ra \(\widehat{D_1}=\widehat{C_1}\)
Xét ΔADC và ΔBCD có:
+ AC = BD (gt)
+ \(\widehat{D_1}=\widehat{C_1}\) (cmt)
+ DC là cạnh chung.
=> ΔADC = ΔBCD (c - g - c)
=> \(\widehat{ADC}=\widehat{BCD}\) (2 góc tương ứng)
Suy ra: ABCD là hình thang cân (đpcm)

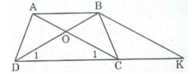
Từ B kẻ đường thẳng song song với AC cắt đường thẳng DC tại K.
Ta có hình thang ABKC có hai cạnh bên BK // AC nên AC = BK
Mà AC = BD (gt)
Suy ra: BD = BK do đó ∆ BDK cân tại B
⇒ ∠ D 1 = ∠ K (tính chất hai tam giác cân)
Ta lại có: ∠ C 1 = ∠ K (hai góc đồng vị)
Suy ra: ∠ D 1 = ∠ C 1
Xét ∆ ACD và ∆ BDC:
AC = BD (gt)
∠ C 1 = ∠ D 1 (chứng minh trên)
CD chung
Do đó ∆ ACD = ∆ BDC (c.g.c) ⇒ ∠ (ADC) = ∠ (BCD)
Hình thang ABCD có ∠ (ADC) = ∠ (BCD) nên là hình thang cân.