
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


5. Dấu hiệu ( định lí ) nhận biết 2 đường thẳng song song:
+ Nếu đường thẳng c cắt hai đường thẳng a,b và trong các góc tạo thành có 1 cặp góc so le trong bằng nhau ( hoặc góc đồng vị bằng nhau ) thì a và b song song với nhau
6. Tiên đề Ơ - clit về đường thẳng song song:
Qua 1 điểm nằm ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó
7, Định lí về hài đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3
Nếu 2 đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3 thì chúng song song với nhau
8. Tính chất ( định lí ) của 2 đường thẳng song song:
Nếu 1 đường thẳng cắt 2 đường thẳng song song thì
1. Hai góc đồng vị bằng nhau
2. Hai góc so le trong bằng nhau
3. Hai góc trong cùng phía bù nhau
5. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song.
\(\widehat{A_1}=\widehat{B}_1\Rightarrow a//b\)
- Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song.
\(\widehat{A}_3=\widehat{B}_1\Rightarrow a//b\)
- Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau thì hai đường thẳng song song.
\(\widehat{A}_2+\widehat{B}_1=180^0\Rightarrow a//b\)
a A 1 2 3 b c 1 B

Xét 2 tg bằng nhau theo TH g.c.g rồi suy ra các cạnh bằng nhau

song song với AB hả bạn. Chứng mik kia là góc hay là tam giác??

Bài giải:
a) Định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia”.
b) Định lí được minh họa bởi hình vẽ sau:
 |
| c vuông góc với a, a // b thì c vuông góc với b |

a) Vì AB//OC
=> OAB = COA
Vì CA//OB
=> CAO = AOB
b) Vì OA là phân giác COB
=> COA = BOA
=> CAO = BAO
=> AO là phân giác CAB

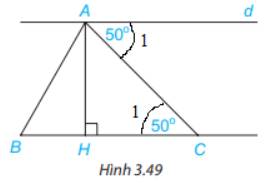
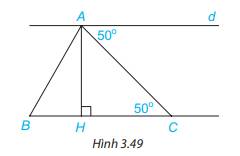
a) Vì \(\widehat {{A_1}} = \widehat {{C_1}}( = 50^\circ )\), mà 2 góc này ở vị trí so le trong nên d // BC (Dấu hiệu nhận biết hai đường thẳng song song )
b) Vì d // BC, mà AH \( \bot \)BC nên d \( \bot \)BC (Đường thẳng vuông góc với một trong hai đường thẳng song song thì cũng vuông góc với đường thẳng kia)
c) Trong các kết luận trên, kết luận a) được suy ra từ dấu hiệu nhận biết hai đường thẳng song song
Kết luận b) được suy ra từ tính chất của hai đường thẳng song song.
1. Ghi nhớ lại các một số kiến thức trong hình học phẳng:
– Trong hình bình hành, hình thoi, hình vuông, hình chữ nhật,…: Các cặp cạnh đối song song với nhau.
– Đường trung bình của tam giác, hình bình hành,…: Đường thẳng đi qua hai trung điểm của cặp cạnh bên (cặp cạnh đối diện).
– Định lý Ta – let đảo: Nếu một đường thẳng cắt hai cạnh của tam giác và định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
2. Ghi nhớ các tính chất:
– Tính chất 1: Trong không gian, qua một điểm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đó.
A ∉ a ⇒ ∃! b: b ⊃ A và a//b
– Tính chất 2: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
a//x; b//x và a ≠ b ⇒ a//b
– Định lý về giao tuyến của ba mặt phẳng:
Nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.
Vậy
1. Nếu ta nhìn thấy được hai đường thẳng đó đồng phẳng thì ta sẽ sử dụng các kiến thức trong hình học phẳng để chứng minh.
2. Nếu ta chưa thấy hai đường thẳng đó đồng phẳng thì có thể áp dụng các tính chất 1, 2 và định lý về giao tuyến của ba mặt phẳng.
9 PHƯƠNG PHÁP CHỨNG MINH HAI ĐƯỜNG THẲNG SONG SONG