Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Lấy ví dụ minh họa đồ thị hình 9.3 (SGK tr. 41).
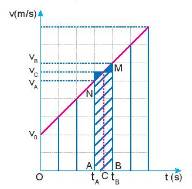
Ta sẽ tính độ dịch chuyển \(d\) của chất điểm có đồ thị vận tốc - thời gian như hình 9.3 trên.
Như đã biết theo đầu bài, độ dịch chuyển của chất điểm có độ lớn bằng với diện tích hình thang giới hạn bởi đồ thị (v - t) và trục tọa độ Ov, Ot.
Từ đồ thị, ta thấy được đáy nhỏ của hình thang có độ lớn là \(v_0\), đáy lớn của hình thang có độ lớn là \(v\) và chiều cao của hình thang có độ lớn là thời gian \(t\).
Công thức tính diện tích hình thang là: \(S=\dfrac{1}{2}\left(a+b\right)h\) với \(a,b,h\) lần lượt là độ dài đáy nhỏ, đáy lớn và chiều cao.
Áp dụng vào bài toán, ta được: \(d=S=\dfrac{1}{2}\left(v+v_0\right)t\)
\(=\dfrac{1}{2}vt+\dfrac{1}{2}v_0t\).
Mà: \(v=v_0+at\), thay vào ta được:
\(d=\dfrac{1}{2}\left(v_0+at\right)t+\dfrac{1}{2}v_0t\)
\(\Rightarrow d=\dfrac{1}{2}v_0t+\dfrac{1}{2}at^2+\dfrac{1}{2}v_0t\)
\(\Rightarrow d=v_0t+\dfrac{1}{2}at^2\) (điều phải chứng minh).
2. Ta có: \(\left\{{}\begin{matrix}v=v_0+at\\d=v_0t+\dfrac{1}{2}at^2\end{matrix}\right.\)
\(\Rightarrow v^2-v_0^2=\left(v+v_0\right)\left(v-v_0\right)\)
\(=\left(v_0+at+v_0\right)\left(v_0+at-v_0\right)\)
\(=at\left(2v_0+at\right)\)
\(=2a\left(v_0t+\dfrac{1}{2}at^2\right)=2ad\) (điều phải chứng minh).

A. v + v0 = √2aS
B. v2 + v02 = 2aS
C. v - v0 = √2aS
D. v2 - v02 = 2aS

1/ Đáp án B
2/
a) Thời gian vật rơi:
\(t=\frac{v}{g}=3\left(s\right)\)
- Độ cao thả vật:
\(h=\frac{1}{2}gt^2=45\left(m\right)\)
b) Quãng đường vật rơi trong giây cuối cùng trước khi chạm đất :
\(\Delta s'=s_3-s_2=25\left(m\right)\)
1.B
2. a) h=\(\dfrac{v^2}{2g}\)=\(\dfrac{30^2}{2.10}\)=45(m)
t=\(\dfrac{v}{g}\)=\(\dfrac{30}{10}\)=3(s)
b) S2s=\(\dfrac{1}{2}\)gt2s2=\(\dfrac{1}{2}\).10.22=20(m)
\(\Delta S\)=S3s-S2s=h-S2s=25(m)

bài 5
+Đổi vận tốc đầu: \(v_0=18km/h=5m/s\)
Quãng đường đi được trong thời gian t (kể từ t = 0): \(S=v_0t+\dfrac{at^2}{2}=5t+\dfrac{at^2}{2}\)
Quãng đường đi được trong 5 giây đầu (t = 5 s)
\(S_5=5.5+\dfrac{5^2a}{2}\)
Quãng đường đi được trong 4 giây đầu (t = 4 s):\(S_4=5.4+\dfrac{4^2a}{2}\)
Quãng đường đi được trong giây thứ 5:
\(\Delta_s=S_5-S_4\Leftrightarrow5,9=5+\dfrac{\left(5^2-4^2\right)a}{2}\Rightarrow a=\left(0,2m/s^2\right)\)

1)
v0=0
Sgiây thứ 3 = 5m \(\Leftrightarrow S_{giâythứ3}=v_0t+\frac{1}{2}at^2-v_0\left(t-1\right)-\frac{1}{2}a\left(t-1\right)^2=v_0+a\left(t-\frac{1}{2}\right)=0+a\left(3-\frac{1}{2}\right)=\frac{5}{2}a\)
=> \(\frac{5}{2}a=5\)
=> a =2\(m/s^2\)
Quãng đường xe đi được sau 10s là:
t =10s => \(s=v_0t+\frac{1}{2}at^2=\frac{1}{2}.2.10^2=100\left(m\right)\)

a/ \(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{P}+\overrightarrow{N}=\overrightarrow{0}\)
\(\Rightarrow F=\mu mg=0,2.1000.10=2000\left(N\right)\)
\(P=F.v=2000.10=20000\left(W\right)\)
b/ \(F=1000+0,2.1000.10=3000\left(N\right)\)
\(v^2-v_0^2=2aS\Leftrightarrow S=150\left(m\right)\)
\(t=\frac{20-10}{1}=10\left(s\right)\)
\(\Rightarrow P=\frac{F.s}{t}=\frac{3000.150}{10}=45000\left(W\right)\)

sách giáo khoa có đó bạn
trả lời các câu khác của tớ nx vứi