K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
26 tháng 3 2017
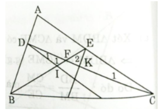
Gọi F là giao điểm của BE và CD.
Ta có DI // AC (gt) ⇒ ∠D1 = ∠C1 (so le trong)
và ∠F1 = ∠F2 (đối đỉnh)
Do đó: ΔDFI ∼ ΔCFE (g.g)
![]()
Tương tự ta có: ΔDFB ∼ ΔKFE
![]()
Từ (1), (2) ⇒ FC.FI = FB.FK
![]()
Do đó theo định lí Talét đảo ta có KI // BC.

3. Chứng minh công thức:
AF/AB + BE/BC + CN/CA = 1 trong tam giác ABC
Giả thiết:
Cách chứng minh:
Trường hợp đặc biệt:
Nếu F, E, N là các điểm chia các cạnh theo cùng một tỉ lệ (ví dụ: F chia AB theo tỉ lệ x, E chia BC theo tỉ lệ y, N chia CA theo tỉ lệ z sao cho x + y + z = 1).
Chứng minh tổng quát:
\(\frac{A F}{A B} + \frac{B E}{B C} + \frac{C N}{C A} = x + y + z\)
Trường hợp đặc biệt:
Nếu F, E, N là trung điểm các cạnh, thì mỗi phân số đều bằng 1/2, tổng lại là 3/2 ≠ 1.
Vậy công thức đúng khi ba điểm chia ba cạnh theo tỉ lệ x, y, z với x + y + z = 1.