Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
Do đó ΔHBA\(\sim\)ΔABC
b: \(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
c: Xét ΔAHB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
hay AD/AC=AE/AB
=>ΔADE\(\sim\)ΔACB

a, Ta có :
^C = 450 ( t/c tam giác vuông cân : mỗi góc nhọn đều bằng 450 ) (*)
Lại có : Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó
Mà : ^BDH = 900 => ^HDA + ^BDH = ^DBA => ^HDA = ^DBA - ^BDH = 1800 - 900 = 900
Suy ra : ^ADE = ^HDE = ^HDA/2 = 900/2 = 450 (**)
tỪ (*); (**) TA CÓ ĐPCM

A B C D E H
a) Tam giác ABC cân tại A có AH là đường cao nên AH đồng thời là đường trung tuyến
=> HB = HC
Xét 2 tgiac vuông: tam giác ABH và tam giác ACH có:
AB = AC (gt)
HB = HC (cmt)
suy ra: tam giác ABH = tam giác ACH (ch_cgv)
=> góc BAH = góc CAH
2) HB = HC = 1/2 BC = 4cm
Áp dụng Pytago ta có:
AH2 + HB2 = AB2
=> AH2 = AB2 - HB2 = 9
=> AH = 3
3) Xét 2 tam giác vuông: tam giác HDB và tam giác HEC có:
BH = CH (cmt)
góc DBH = góc ECH (gt)
suy ra: tam giác HDB = tam giác HEC (ch_gn)
=> HD = HE
=> tam giác HDE cân tại H

a: Xét tứ giác ADHE co
góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
b: IO//AC
AC vuông góc HE
=>IO vuông góc HE
mà ΔOEH cân tại O
nên góc EOI=góc HOI
Xét ΔEOI và ΔHOI có
OE=OH
góc EOI=góc HOI
OI chung
Do đó: ΔEOI=ΔHOI
=>góc EIO=góc HIO
=>IO là phân giác của góc EIH

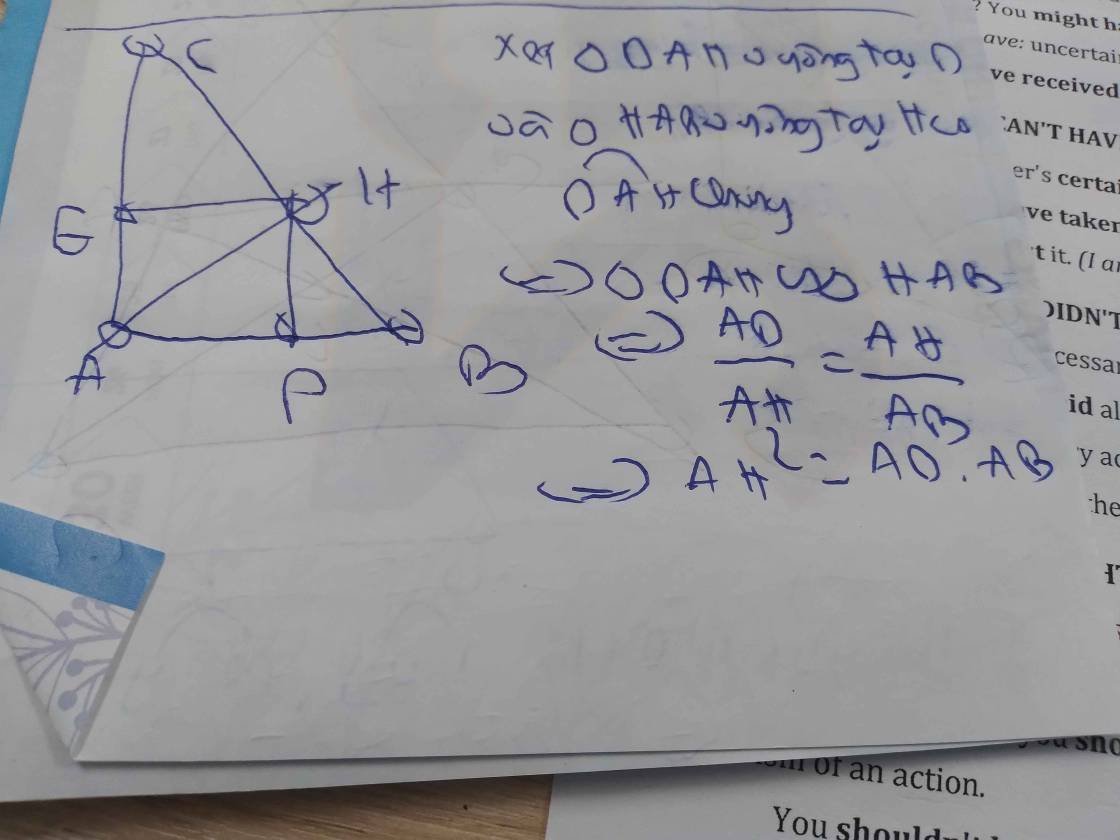
a: Xet ΔHBA và ΔABC có
góc BHA=góc BAC
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: ΔABC vuông tại A có AH vuông góc BC
nên BA^2=BH*BC
\(AB=\sqrt{3\cdot12}=6\left(cm\right)\)
\(AH=\sqrt{6^2-3^2}=3\sqrt{3}\left(cm\right)\)
c: Xet ΔCAE có KD//AE
nên KD/AE=CK/CE
Xét ΔCEB có KH//EB
nên KH/EB=CK/CE=KD/AE
mà AE=EB
nên KH=KD
Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
=>\(\widehat{ADE}=\widehat{AHE}\)
mà \(\widehat{AHE}=\widehat{C}\left(=90^0-\widehat{HAC}\right)\)
nên \(\widehat{ADE}=\widehat{C}\)
Xét tứ giác ` AEHD` có:
\(\widehat{DAE}=\widehat{AEH}=\widehat{HDA}=90^o\)
=> Tứ giách `AEHD` là hình chữ nhật
=> `AH = DE`
Gọi `O` là giao điểm của` AH` và `DE`
=> `O` là trung điểm của `AH` và `DE`
=> \(\left\{{}\begin{matrix}OA=\dfrac{1}{2}AH\\OD=\dfrac{1}{2}DE\end{matrix}\right.\)
Mà `AH = DE` (Chứng minh trên)
=> `OA = OD`
Xét `ΔOAD` có: `OA = OD`
=> `ΔOAD` cân tại `O`
=> \(\widehat{ODA}=\widehat{OAD}\)
Ta có: \(\widehat{C}=\widehat{DAO}\) (cùng phụ với \(\widehat{HAC}\))
=> \(\widehat{C}=\widehat{ADO}\)
Hay \(\widehat{C}=\widehat{ADE}\) `(ĐPCM)`