
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


giả sử vs a>1 nên tồn tại số nguyên tố p sao cho p|a
ta có p | n!+1 và p | (n+1)!+1 nên p | (n+1)!-n!
hay p | n.n! nên p là số nguyên tố bé hơn n
nên p | n! mà p| n! +1 .mâu thuẫn
vậy giả sử sai. nên
giả sử vs a>1 nên tồn tại số nguyên tố p sao cho p|a
ta có p | n!+1 và p | (n+1)!+1 nên p | (n+1)!-n!
hay p | n.n! nên p là số nguyên tố bé hơn n
nên p | n! mà p| n! +1 .mâu thuẫn
vậy giả sử sai. nên

cộng H(x)với G(x)
H(x)+G(x)=(x^3-2x^2+3x-1)+(-x^3+3x^2-3x+3)
=x^3-2x^2+3x-1-x^3+3x^2-3x+3
=x^2+2
mà x^2 lớn hơn hoặc bằng 0
nên x^2+2 lớn hơn 0
suy ra đa thức H(x) và G(x) không có nghiệm chung nào

tọa độ M thỏa mãn phương trình tham số của d với t = -1
Tọa độ M thỏa mãn phương trình tham số của d’ với t = -1
⇒ M là điểm chung của d và d’

Lấy một đỉnh B tùy ý của hình đa diện (H). Gọi M 1 là một mặt của hình đa diện (H) chứa B. Gọi A, B, C là ba đỉnh liên tiếp của M 1 . Khi đó AB, BC là hai cạnh của (H). Gọi M 2 là mặt khác với M 1 và có chung cạnh AB với M 1 . Khi đó M 2 còn có ít nhất một đỉnh D sao cho A, B, D là ba đỉnh khác nhau liên tiếp của M 2 . Nếu D ≡ C thì M 1 và M 2 có hai cạnh chung AB và BC, điều này vô lí. Vậy D phải khác C. Do đó qua đỉnh B có ít nhất ba cạnh BA, BC và BD.

Chọn C
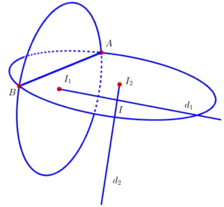
Gọi d1 là đường thẳng đi qua I1 và vuông góc với mặt phẳng (ABI1), khi đó d1 chứa tâm các mặt cầu đi qua đường tròn tâm I1; d2 là đường thẳng đi qua I2 và vuông góc với mặt phẳng (ABI2), khi đó d2 chứa tâm các mặt cầu đi qua đường tròn tâm I2.
Do đó, mặt cầu (S) đi qua cả hai đường tròn tâm (I1) và (I2) có tâm I là giao điểm của d1 và d2 và bán kính R = IA



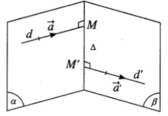
Phương trình tham số của đường thẳng d: 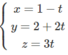
Vecto chỉ phương của hai đường thẳng d và d’lần lượt là a → = (−1; 2; 3), a ' → = (1; −2; 0).
Xét điểm M(1 – t; 2 + 2t; 3t) trên d và điểm M’(1 + t’; 3 – 2t’; 1) trên d’ ta có MM ' → = (t′ + t; 1 − 2t′ − 2t; 1 − 3t).
MM’ là đường vuông góc chung của d và d’.
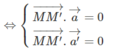
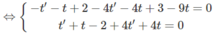
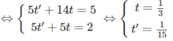
Thay giá trị của t và t’ vào ta được tọa độ M và M’ là
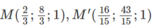
Do đó MM'→ = 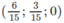
Suy ra đường vuông góc chung Δ của d và d’ có vecto chỉ phương u → = (2; 1; 0)
Vậy phương trình tham số của
∆
là: 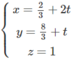






minh dang can gappppp