Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{1+2+1}{3}=\dfrac{4}{3}\\y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{-2-1+1}{3}=-\dfrac{2}{3}\\z_G=\dfrac{z_A+z_B+z_C}{3}=\dfrac{0+1+0}{3}=\dfrac{1}{3}\end{matrix}\right.\Rightarrow G\left(\dfrac{4}{3};-\dfrac{2}{3};\dfrac{1}{3}\right)\)
\(\overrightarrow{CD}\left(-1;-3;0\right)\) la vecto phap tuyen cua mp do
\(\Rightarrow\left(P\right):-1\left(x-\dfrac{4}{3}\right)-3\left(y+\dfrac{2}{3}\right)+0=0\Leftrightarrow x+3y+\dfrac{2}{3}=0\)

Chọn A.

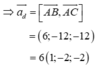
Đường thẳng d đi qua G(2;-1;0) và có vectơ chỉ phương là ![]()
Vậy phương trình tham số của d là 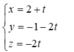

Đáp án A.
(P) đi qua A và G nên (P) đi qua trung điểm của BC là điểm 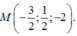
Ta có: 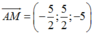 cùng phương với véc tơ (-1;1;-2)
cùng phương với véc tơ (-1;1;-2)
Mặt phằng (ABC) có vác tơ pháp tuyến:
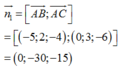
cùng phương với véc tơ (0;2;1)
Vì (P) chứa AM và vuông góc với (ABC) nên (P) có véc tơ chỉ phương:
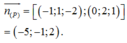
Ngoài ra (P) qua A ( 1 ; - 2 ; 3 ) nên phương trình (P):
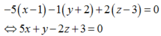

Đáp án B
Phương pháp: (P) cách đều B, C
![]()
TH1: BC//(P)
TH2: I ∈ (P)với I là trung điểm của BC.
Cách giải:
![]()
(P) cách đều B, C
![]()
TH1: BC//(P)
![]()
=> (P) đi qua O và nhận b → = ( 6 ; - 3 ; - 4 ) là 1 VTPT
![]()
TH2: I ∈ (P) với I là trung điểm của BC.
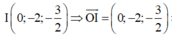
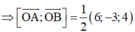
![]()
Dựa vào các đáp án ta chọn được đáp án B.

Chọn A
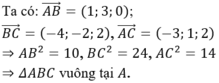
Tâm I của đường tròn ngoại tiếp tam giác là trung điểm của BC => I (0; 2; 0)
Đường thẳng d cần tìm đi qua I (0; 2; 0) và nhận vectơ ![]() làm véc tơ chỉ phương. Phương trình chính tắc của đường thẳng d là
làm véc tơ chỉ phương. Phương trình chính tắc của đường thẳng d là ![]()
\(G\left(\dfrac{4}{3};-\dfrac{2}{3};\dfrac{1}{3}\right)\) ; \(\overrightarrow{DC}=\left(1;3;1\right)\)
Pt mặt phẳng qua G vuông góc CD và nhận \(\overrightarrow{DC}\) là 1 vtpt có dạng:
\(1\left(x-\dfrac{4}{3}\right)+3\left(y+\dfrac{2}{3}\right)+1\left(z-\dfrac{1}{3}\right)=0\)
\(\Leftrightarrow x+3y+z-\dfrac{1}{3}=0\)