Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{1+3x}{\sqrt{2x^2+3}}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{3+\dfrac{1}{x}}{\sqrt{2+\dfrac{3}{x^2}}}=\dfrac{3+0}{\sqrt{2+0}}=\dfrac{3}{\sqrt{2}}\)
\(=\dfrac{3\sqrt{2}}{2}\)

Trình bày công thức các thứ khá dài nên tôi thử nói hướng, nếu bạn hiểu đc và làm đc thì ok còn nếu k hiểu thì bảo mình, mình làm full cho
Bây giờ phân tích mẫu trước, ra (x-1)2(x+2)
Để cái lim này nó ra đc 1 số thực thì tử và mẫu cùng phải triệt tiêu (x-1)2 đi, tức là tử phải chia hết (x-1)2, tức là tử cũng phải có nghiệm kép x=1
Do đó \(\left\{{}\begin{matrix}f\left(1\right)=0\\f'\left(1\right)=0\end{matrix}\right.\)

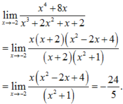

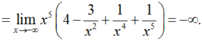
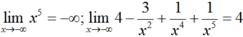
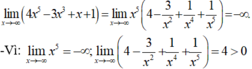
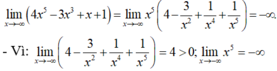
Chọn B.
Ta có: