Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
Xét tứ giác BDNC có
DN//BC
BD//NC
Do đó: BDNC là hình bình hành
b: Xét tứ giác BDNH có BH//DN
nên BDNH là hình thang

Hướng dẫn a,b
Tự vẽ hình
a) M , N là trung điểm AB , AC => MN là đường trung bình của tam giác ABC
=> MN//BC => DN//BC . Mà BD// NC => Tứ giác BDNC là hbh
b) Có \(\widehat{NCH}=\widehat{NDB}\) ( hình bình hành )
Tam giác AHC vuông có trung tuyến HN = 1/2 AC = NC => Tam giác NHC cân => \(\widehat{NCH}=\widehat{NHC}\)
=> \(\widehat{NDB}=\widehat{NHC}\)
Mà NHC = NHD (so le trong ) = > NHD = NBD
=> BDNH là hình thang cân

a) Xét ΔAEC có
H là trung điểm của EC(E và C đối xứng với nhau qua H)
D là trung điểm của AC(gt)
Do đó: HD là đường trung bình của ΔAEC(Định nghĩa đường trung bình của tam giác)
⇒HD//AE và \(HD=\dfrac{AE}{2}\)(Định lí 2 về đường trung bình của tam giác)
b) Ta có: HD//AE(cmt)
mà I∈HD(gt)
nên AE//IH
Ta có: AI//BC(gt)
mà H∈BC
và E∈BC
nên AI//EH
Xét tứ giác AEHI có
AI//EH(cmt)
AE//HI(cmt)
Do đó: AEHI là hình bình hành(Dấu hiệu nhận biết hình bình hành)

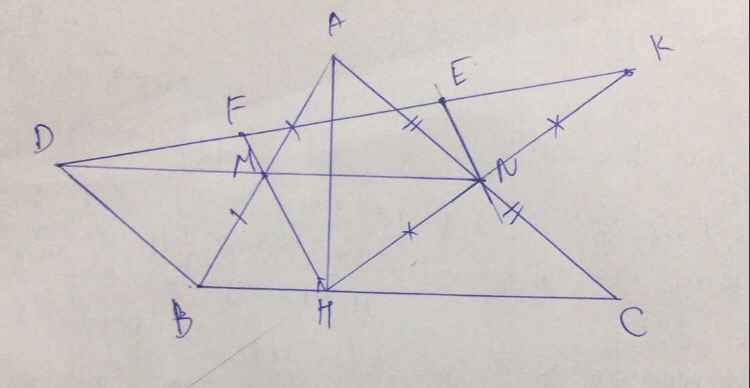
a: Xét ΔHAB có
M là trung điểm của HA
N là trung điểm của HB
Do đó: MN là đường trung bình
=>MN//AB
hay ABNM là hình thang

Câu c: Ta sẽ cm góc BDN = góc HND ( vì cùng bằng góc AND)
Thật vậy: BDN = AND slt
HND = AND (dễ cm tam giác ANH cân tại N, AH dễ cm là đường cao, nên đồng thời là phân giác)
Þtứ giác BHND là hình thang cân
Câu d: Gọi I là giao điểm của HM và DK
Xét tứ giác ADBN có
BD = AN (=HN vì BHND là hình thang cânÞ BD = HN, AHCK là hcn ÞAN = HN)
suy ra Tứ giác ADBN là hbh ÞM là trung điểm của DN suy ra MD = MN
Xét tam giác EDN có MI song song EN, MD = MN (cmt)suy ra MI là đường trung bình hay ID = IE (1)
Tương tự xét tam giác KIH có NE là đường trung bình hay EK = IE (2)
Từ (1) và (2) suy ra ID = IE = EK. Vậy DE = 2EK
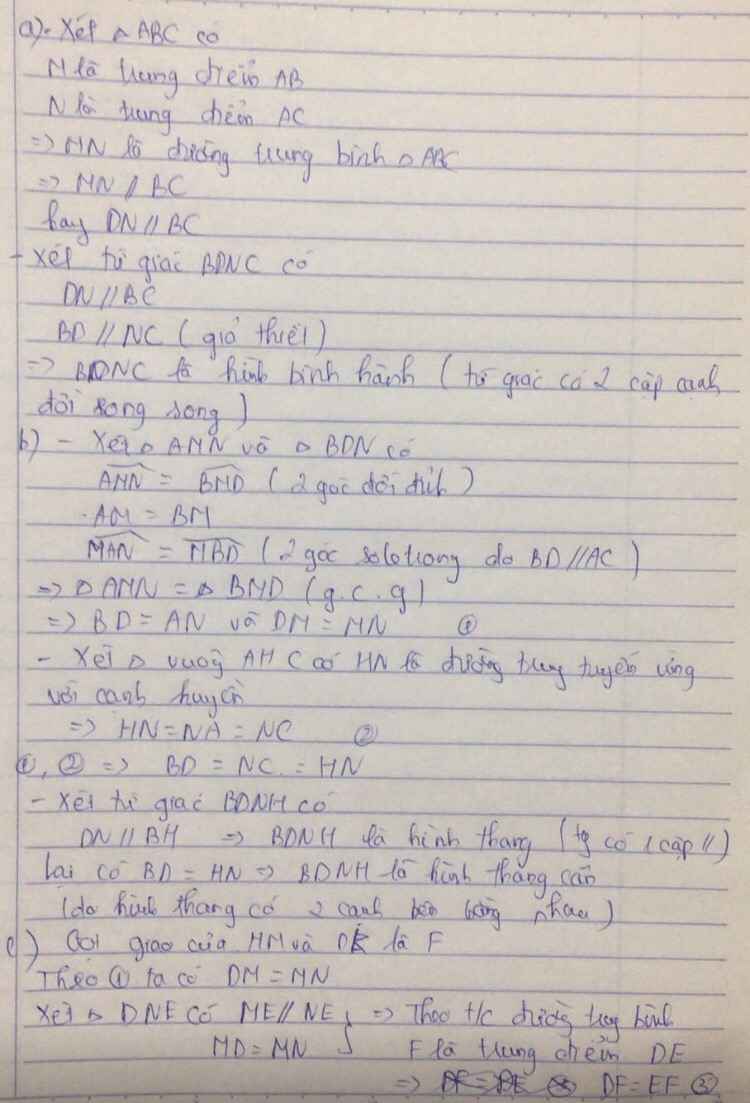
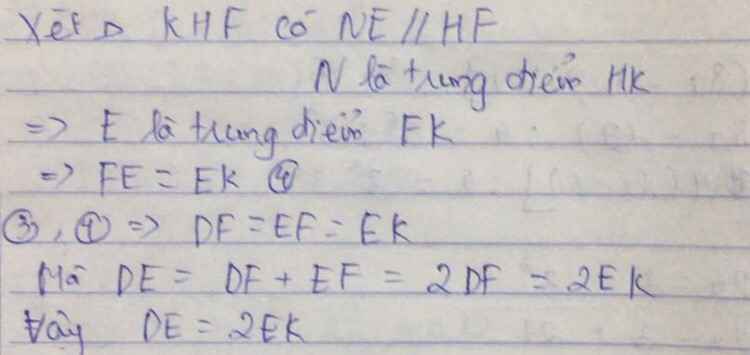
a: Xét ΔABC có AM/AB=AN/AC
nên MN//BC và MN=1/2BC
=>ND//BC
Xét tứ giác BDNC có
BD//NC
DN//BC
DO đó; BDNC là hình bình hành
b: Ta có: ΔAHB vuông tại H
mà HM là trung tuyến
nên HM=AM(1)
Ta có: ΔAHC vuông tại H
mà HN là trung tuyến
nên HN=AN(2)
Từ (1) và (2) suy ra MN là trung trực của AH
=>DN là trung trực của AH
=>DA=DH
mà DA=NB
nên DH=NB
Xét tứ giác DBHN có
DN//BH
DH=NB
DO đó: DBHN là hình thang cân